Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
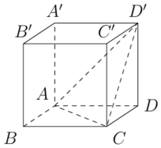
Gọi x là độ dài cạnh của hình lập phương. Có:
A C = A D ' = C D ' = x 2 ⇒ S A C D ' = x 2 3 4 ⇔ x 2 3 4 = a 2 3 ⇔ x = 2 a
Vậy V=x3=(2a)3=8a3

Đáp án là B

Gọi x là độ dài của cạnh hình lập phương
Ta có: 

Theo giả thiết, 
![]()
Vậy thể tích lập phương là: ![]()

Chọn A
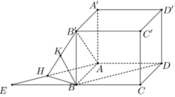
Trên mặt đáy (ABCD) dựng hình bình hành AEBD như hinhd vẽ, Gọi H, K lần lượt là hình chiếu của B lên AE, B’H.
Khi đó
![]()
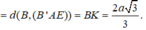
![]()
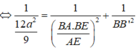
![]()

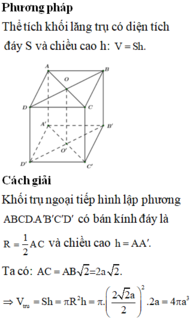



Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)