Vẽ các đường thẳng sau trên cùng một hệ trục tọa độ, sau đó tính khoảng cách từ gốc O đến các đường thẳng đó
a) \(y=2-x\)
b) \(y=2x+1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 12 2023
a:
Vẽ đồ thị y=2-x
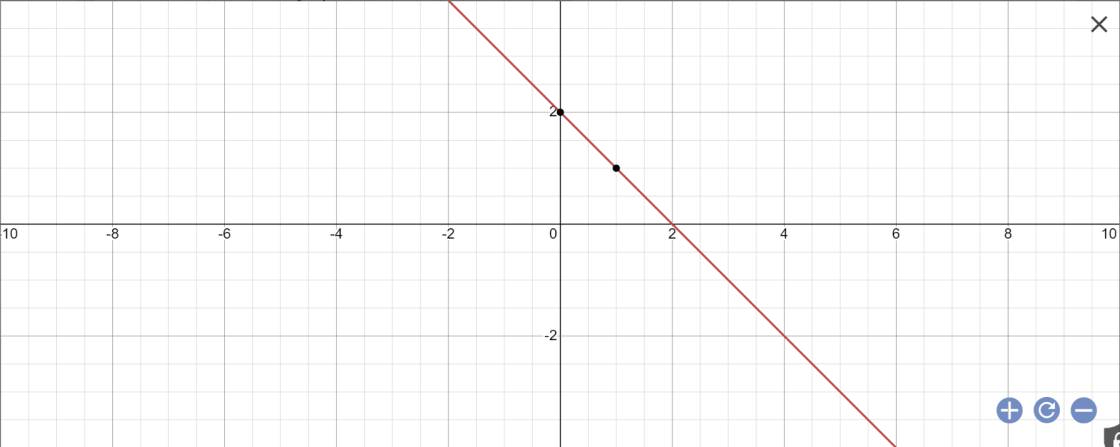
y=2-x
=>y+x-2=0
=>x+y-2=0
Khoảng cách từ O đến đường thẳng x+y-2=0 là:
\(d\left(O;x+y-2=0\right)=\dfrac{\left|0\cdot1+0\cdot1-2\right|}{\sqrt{1^2+1^2}}\)
\(=\dfrac{2}{\sqrt{1+1}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
b:
Vẽ đồ thị y=2x+1
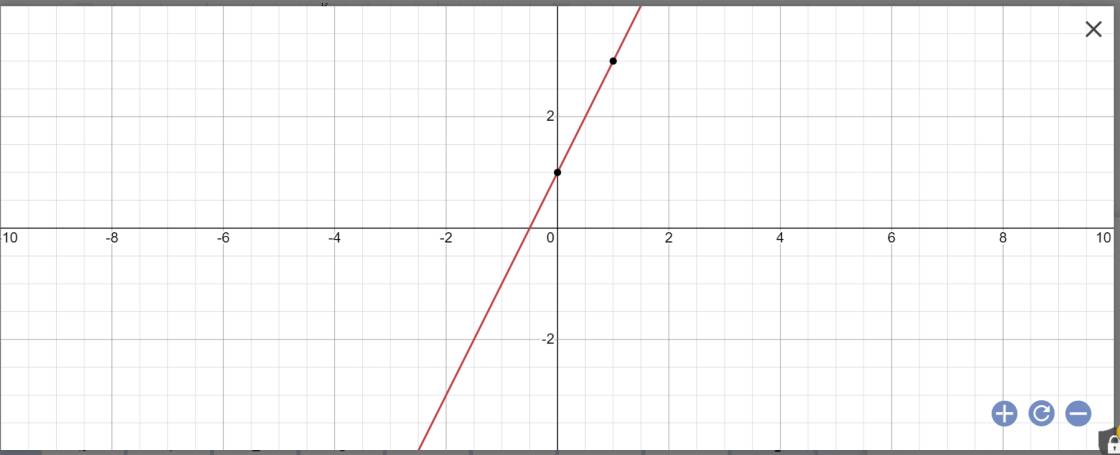
y=2x+1
=>2x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng y=2x+1 là:
\(\dfrac{\left|0\cdot2+0\cdot\left(-1\right)+1\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{4+1}}=\dfrac{\sqrt{5}}{5}\)
c:
Vẽ đồ thị \(y=\dfrac{x-2}{2}\)
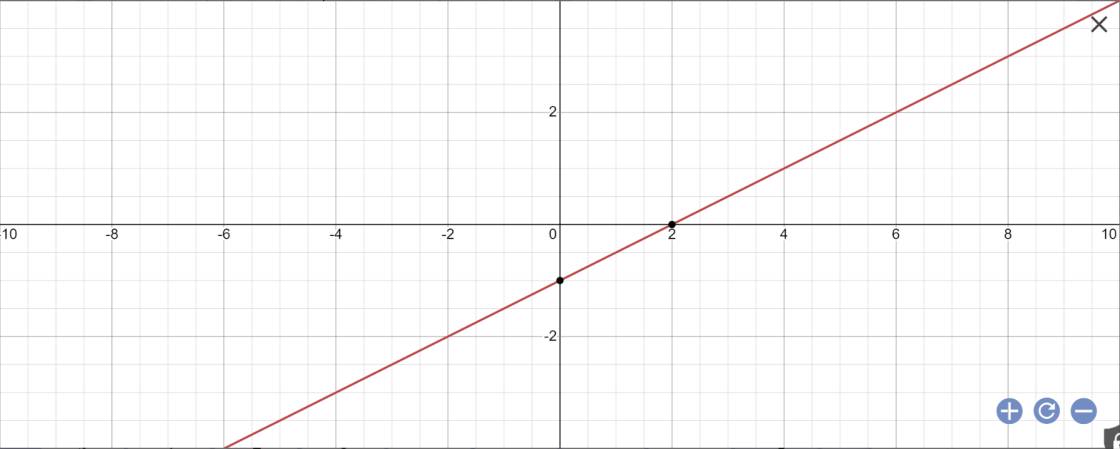
\(y=\dfrac{x-2}{2}\)
=>x-2=2y
=>x-2y-2=0
Khoảng cách từ O(0;0) đến đường thẳng \(y=\dfrac{x-2}{2}\) là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-2\right)-2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\dfrac{\left|-2\right|}{\sqrt{1+4}}=\dfrac{2}{\sqrt{5}}\)
d:
Vẽ đồ thị y=-2x
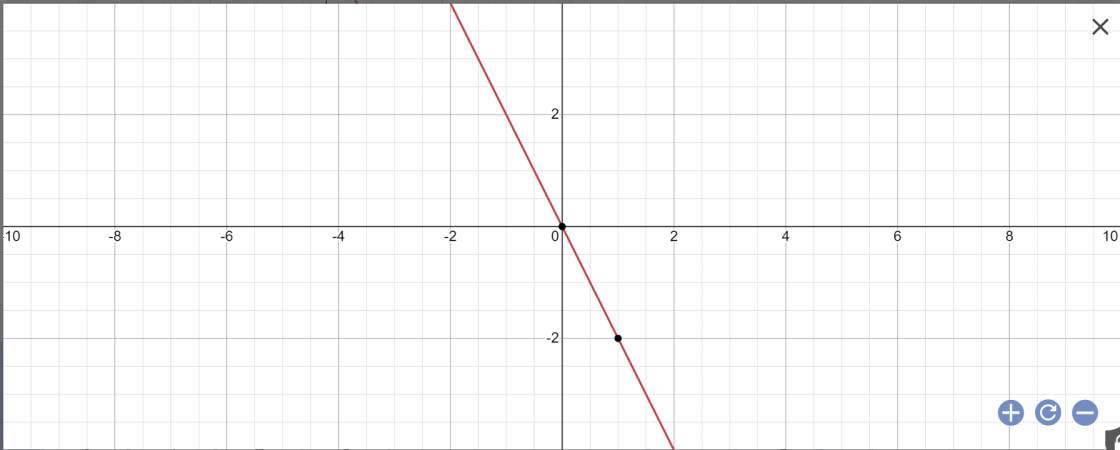
y=-2x
=>-2x+y=0
Khoảng cách từ O(0;0) đến đường thẳng y=-2x là:
\(\dfrac{\left|0\cdot\left(-2\right)+0\cdot1+0\right|}{\sqrt{\left(-2\right)^2+1^2}}=\dfrac{0}{\sqrt{\left(-2\right)^2+1^2}}=0\)
2 tháng 12 2023
a:
Vẽ đường thẳng y=-3x-3
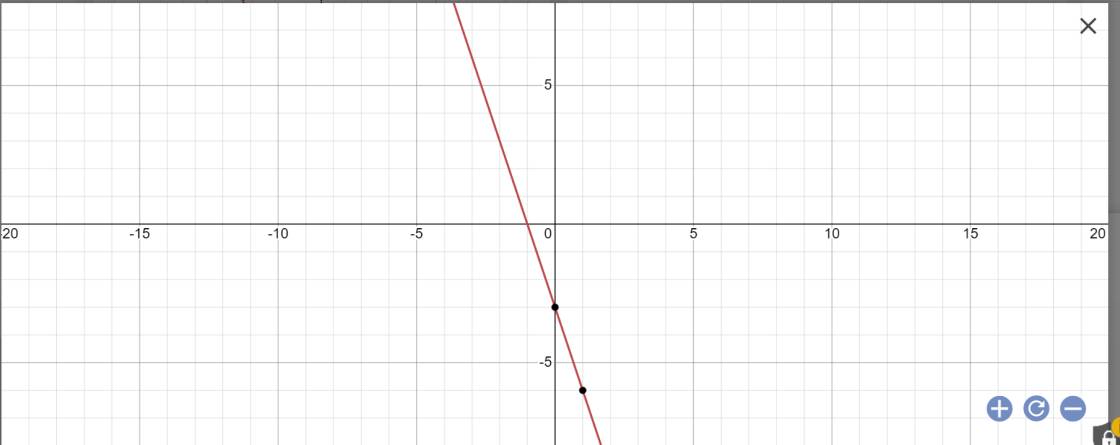
y=-3-3x
=>3x+y+3=0
Khoảng cách từ O đến đường thẳng y=-3x-3 là:
\(\dfrac{\left|0\cdot3+0\cdot1+3\right|}{\sqrt{3^2+1^2}}=\dfrac{3}{\sqrt{10}}\)
b:
Vẽ đường thẳng y=x
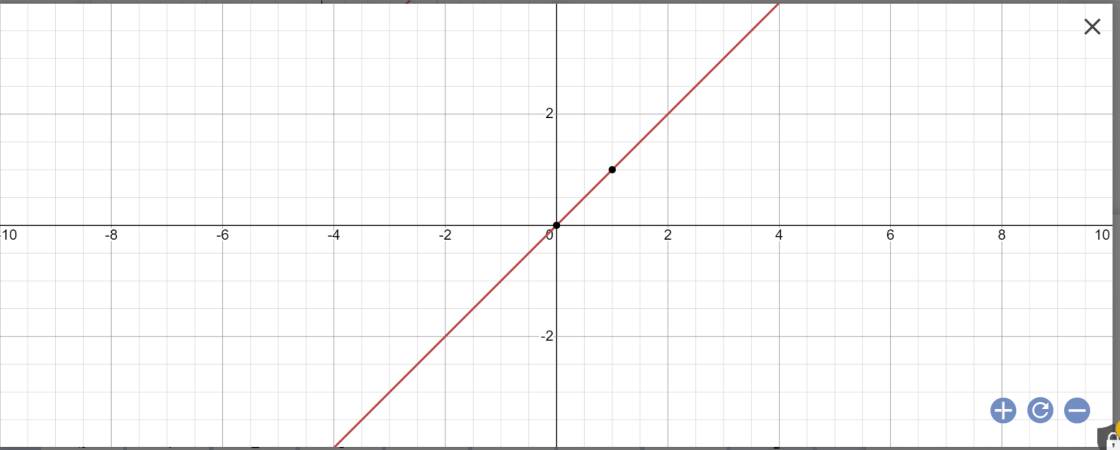
y=x
=>x-y=0
Khoảng cách từ O(0;0) đến đường thẳng y=x là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+0\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{0}{\sqrt{2}}=0\)
c:
Vẽ đồ thị y=-x
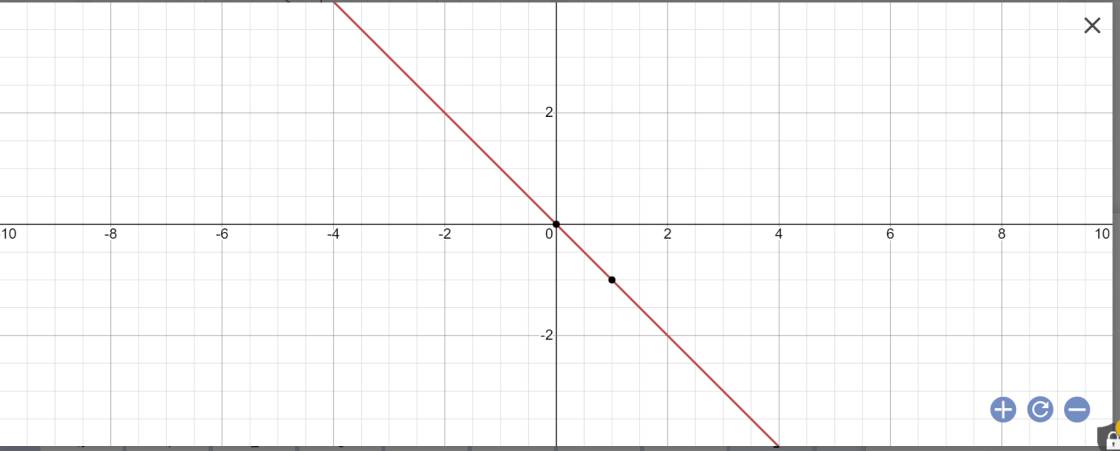
y=-x
=>x+y=0
Khoảng cách từ O(0;0) đến đường thẳng y=-x là:
\(\dfrac{\left|0\cdot1+0\cdot1+0\right|}{\sqrt{1^2+1^2}}=0\)
d:
Vẽ đồ thị hàm số y=1/2x
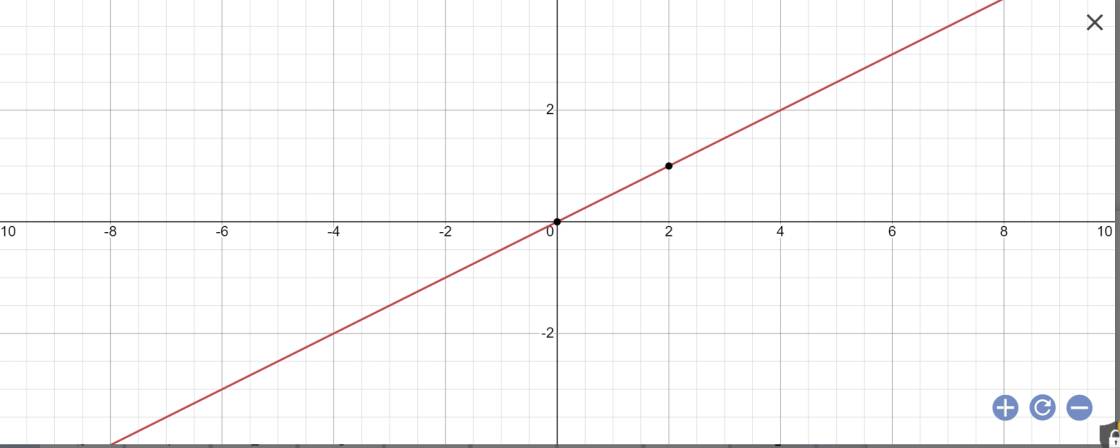
y=1/2x
=>1/2x-y=0
Khoảng cách từ O(0;0) đến đường thẳng y=1/2x là:
\(\dfrac{\left|0\cdot\dfrac{1}{2}+0\cdot\left(-1\right)+0\right|}{\sqrt{\left(\dfrac{1}{2}\right)^2+\left(-1\right)^2}}=\dfrac{0}{\sqrt{\dfrac{1}{4}+1}}=0\)
7 tháng 1 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+1=-2x+4\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
8 tháng 1 2022
b: Tọa độ là:
\(\left\{{}\begin{matrix}x+1=-2x+4\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
8 tháng 1 2022
c: Gọi A,B lần lượt là tọa độ giao điểm của đường thẳng y=-2x+4 đến trục Ox, Oy
Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\-2x+4=0\end{matrix}\right.\Leftrightarrow A\left(2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x_B=0\\y_B=-2\cdot0+4\end{matrix}\right.\Leftrightarrow B\left(0;4\right)\)
Gọi OH là khoảng cách từ O đến đường thẳng y=-2x+4
Xét ΔOAB vuông tại O có OH là đường cao
nên \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
hay \(OH=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)
16 tháng 12 2021
\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
VH
2 tháng 10 2020
a, \(y=2-x\left(d\right)\)
\(x=0\Rightarrow y=2\Rightarrow A\left(0;2\right)\in\left(d\right)\Rightarrow OA=2\)
\(x=2\Rightarrow y=0\Rightarrow B\left(2;0\right)\in\left(d\right)\Rightarrow OB=2\)
Gọi H là chân đường vuông góc kẻ từ O lên \(\left(d\right)\)
Ta có: \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{4}+\frac{1}{4}=\frac{1}{8}\Rightarrow OH=2\sqrt{2}\)
b, \(y=2x+1\left(d'\right)\)
\(x=0\Rightarrow y=1\Rightarrow B'\left(0;1\right)\in\left(d'\right)\Rightarrow OB'=1\)
\(x=-\frac{1}{2}\Rightarrow y=0\Rightarrow A'\left(-\frac{1}{2};0\right)\in\left(d\right)\Rightarrow OA'=\frac{1}{2}\)
Gọi H' là chân đường vuông góc kẻ từ O lên \(\left(d\right)\)
Ta có: \(\frac{1}{OH'^2}=\frac{1}{OA'^2}+\frac{1}{OB'^2}=\frac{1}{\frac{1}{4}}+\frac{1}{1}=5\Rightarrow OH'=\frac{\sqrt{5}}{5}\)
Bạn nhớ đăng sớm nha muộn quá mình ít on lắm
a
Hãy tự vẽ hình nha
Để tính khoảng cách hãy chọn giá trị x và y = 0 để dễ nhìn
x = 0 ; y = 2
y = 0 ; x = 2
Vẽ hình ra đặt tên hai tọa độ 2 điểm là A và B
Khi đó độ dài A là trị tuyệt đó của A là 2
Độ dài B là trị tuỵet đối B là 2
Tam giác OAB vuông
AB^2 = OA^2 + OB^2
AB = căn ( OA^2 + OB^2 )
AB = căn ( 2^2 + 2^2 ) = căn 8 = 2 căn 2 ( Py ta go )
Khoảng cách giữa đường với gốc tọa độ O là 1 đường thẳng vuông góc đi qua gốc tọa độ O vuông góc AB
Vẽ đường cao AC
Sử dụng hệ thức lượng
OC nhân AB = AO nhân BO
OC x 2 căn 2 = 2 x 2
OC = căn 2
Vậy khoảng cách từ gốc tọa độ đến đường thẳng đó là căn 2
b
Giống vậy
Thế x = 0 ; y = 1
y = 0 ; x = -1/2
Vẽ hình đặt 2 toạ độ là C và D
Khi đó độ dài OC = trị tuyệt đối C = 1
Độ dài OD bằng trị tuyệt đối D = 1/2
Tam giác OCD vuông tại O
CD^2 = OC^2 + OD^2
CD = căn ( 1^2 + (1/2)^2 )
CD = căn ( 5/4 ) = ( căn 5 ) / 2 ( Py ta go )
Khoảng cách từ O đến CD là 1 đường thẳng qua góic O vuông góc với CD
Vẽ đường cao OE
Sử dụng hệ thức lượng
OE nhân BC = OB nhân OC
OE x ( căn 5 ) / 2 = 1 x 1/2
OE x ( căn 5 ) / 2 = 1/ 2
OE = ( căn 5 ) / 5
Vậy khoảng cách từ gốc tọa độ đến đường thẳng đó là ( căn 5 ) / 5