Cho d1: x-5y+7=0
d2:5x-y-13=0
d3:5x-y+8=0
a. Tìm phép đối xứng biến d1 thành d2
b. tìm phép đối xứng biến d2 thành d3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:
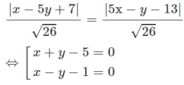

a) Thay hoành độ và tung độ của A vào 2 pt đường thẳng (d1) và (d2), ta lần lượt được:
\(1=3\left(-1\right)+4\) (luôn đúng)
\(-1-2.1=0\) (vô lí)
Như vậy, \(A\in d_1;A\notin d_2\)
b) Gọi giao điểm của d1, d2 là \(B\left(x_0;y_0\right)\). Khi đó \(x_0,y_0\) là các số thỏa mãn \(\left\{{}\begin{matrix}y_0=3x_0+4\\x_0-2y_0=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=6y_0+4\\x_0=2y_0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=-\dfrac{4}{5}\\x_0=-\dfrac{8}{5}\end{matrix}\right.\)
Vậy giao điểm của d1 và d2 là \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
c) Để đường thẳng d1, d2, d3 đồng quy thì d3 phải đi qua giao điểm của d1 và d2. Nói cách khác, d3 phải đi qua điểm \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
\(\Leftrightarrow\left(m-1\right).\dfrac{-8}{5}+\left(m-2\right).\dfrac{-4}{5}+m+1=0\)
\(\Leftrightarrow\dfrac{21}{5}-\dfrac{7}{5}m=0\)
\(\Leftrightarrow m=3\)
Vậy \(m=3\) thỏa mãn ycbt.

a:
b: Phương trình hoành độ giao điểm là:
\(2x+1=x-3\)
=>\(2x-x=-3-1\)
=>x=-4
Thay x=-4 vào y=x-3, ta được:
\(y=-4-3=-7\)
Vậy: Tọa độ giao điểm của (D1) và (D2) là B(-4;-7)
c: Đặt phương trình đường thẳng (d3): y=ax+b
Vì (d3)//(d1) nên \(\left\{{}\begin{matrix}a=2\\b< >1\end{matrix}\right.\)
Vậy: y=2x+b
Thay x=1 và y=0 vào y=2x+b, ta được:
\(b+2\cdot1=0\)
=>b+2=0
=>b=-2
Vậy: (d): y=2x-2

Dễ thấy d và d' không song song với nhau.
Do đó trục đối xứng Δ của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'.
Từ đó suy ra Δ có phương trình:
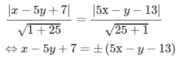
Từ đó tìm được hai phép đối xứng qua các trục:
Δ 1 có phương trình: x + y – 5 = 0,
Δ 2 có phương trình: x – y – 1 = 0.

Khó
a) d1 \(\ne\)d2\(\ne\)d3(1)
Giao d1 và d2 là : \(\int^{x+3y=1}_{2x-y=-5}\Leftrightarrow\int^{x=-2}_{y=1}\)(2)
Giao d1 và d3 là : \(\int^{x+3y=1}_{-3x+2y=8}\Leftrightarrow\int^{x=-2}_{y=1}\)(3)
(1)(2)(3) => dpcm
b) tương tự
hehehehehe mình cũng làm dc hahahahah

Lời giải:
Phép tịnh tiến qua vecto $v$ biến $(d_3)$ thành chính nó thì $\overrightarrow{v}$ vecto chỉ phương của $(d_3)$
$\Rightarrow \overrightarrow{v}=(a,0)$
$T_{\overrightarrow{v}}(d_1)=d_2$
\(\Rightarrow \left\{\begin{matrix} 2x-y+2=0\\ 2(x+a)-y+1=0\end{matrix}\right.\Rightarrow a=\frac{1}{2}\)
Vậy $\overrightarrow{v}=(\frac{1}{2}, 0)$

Chọn D.
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2