một người đứng trên đỉnh một ngọn tháp quan sát thấy 1 người đi xe máy đang tiến về phía chân tháp dưới góc nâng 30 độ. hai phút sau, người đó lại thấy người chạy xe máy dưới góc nâng là 60 độ. hỏi bao lâu sau thời điểm đó, người chạy xe máy tới được chân tháp?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2023
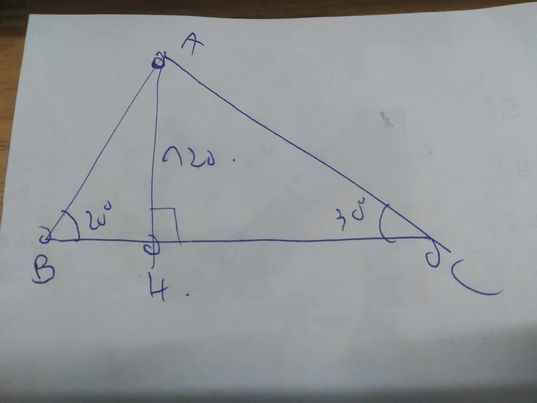
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát
14 tháng 7 2023
7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 9 2021
B: Là vị trí thuyền hiện tại
D: là vị trí thuyền sau 10 phút
AC: chiều cao ngọn hải đăng = 63 m
Xét tg vuông ABC
\(\tan\widehat{ABC}=\tan19^o=\frac{AC}{AB}=\frac{63}{AB}\Rightarrow AB=\frac{63}{\tan19^o}\)
Xét tg vuông ACD có
\(\tan\widehat{ADC}=\tan54^o=\frac{AC}{AD}=\frac{63}{AD}\Rightarrow AD=\frac{63}{\tan54^o}\)
Quãng đường thuyền đi được sau 10' là
\(BD=AB-AD=\frac{63}{\tan19^o}-\frac{63}{\tan54^o}\)
8 tháng 10 2021
Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)