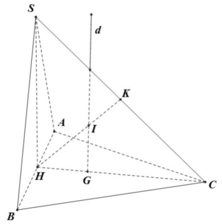
Trong mặt phẳng Oxy, cho tam giác ABC có A(2;3),I(6;6),J(4;5) lần lượt là tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC. Tìm phương trình đường thẳng BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
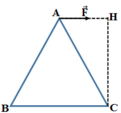
Cánh tay đòn của lực F → là CH. Do đó momen của lực F → đối với trục quay đi qua C và vuông góc với mặt phẳng khung là: MF/C = F.CH = Fℓ 3 /2.

Chọn D.
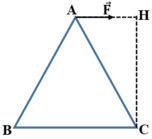
Cánh tay đòn của lực F ⇀ là CH. Do đó momen của lực F→ đối với trục quay đi qua C và vuông góc với mặt phẳng khung là:
M F / C = F.CH = F . l 3 / 2

a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)