Cho Tam giác ABC có 3 đường trung tuyến AM,BN,CP đồng qui tại trọng tâm G. Chứng minh MA<MP+MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC

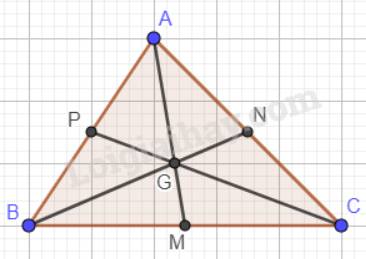
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).

a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên SAGP = SPGB
Tương tự, ta có: SBGM = SMGC và SCGN = SNGA.
Vì G là trọng tâm DABC Þ AG = 2GM.
Þ SBGM = 1 2 SABG Þ SBGM = SAGP = SPGB.
Chứng minh tương tự, ta suy ra được:
SAGP = SPGB = SBGM = SMGC = SCGN = SNGA
b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6 SABC, từ đó suy ra ĐPCM.
Trên tia đối của tia MA lấy điểm E sao cho MA=ME
Xét ΔABM và ΔECM có
AM=EM(theo cách vẽ)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
BM=CM(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
Do đó: ΔABM=ΔECM(c-g-c)
⇒AB=CE(hai cạnh tương ứng)
Xét ΔACE có AE<AC+CE(Bất đẳng thức trong tam giác)
mà CE=AB(cmt)
nên AE<AC+AB(1)
Ta có: MA=ME(theo cách vẽ)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
hay \(AE=2\cdot AM\)(2)
Từ (1) và (2) suy ra \(2\cdot AM< AB+AC\)
\(\Leftrightarrow AM< \frac{AB+AC}{2}=\frac{AB}{2}+\frac{AC}{2}\)(3)
Xét ΔABC có
M là trung điểm của BC(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
P là trung điểm của AB(CP là đường trung tuyến ứng với cạnh AB của ΔABC)
Do đó: MP là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MP=\frac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(4)
Xét ΔABC có
M là trung điểm của BC(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
N là trung điểm của AC(BN là đường trung tuyến ứng với cạnh AC của ΔABC)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MN=\frac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)(5)
Từ (3), (4) và (5) suy ra MA<MP+MN(đpcm)
Cảm ơn bạn