Giá trị nhỏ nhất của hàm số y: \(sin^2x-4sinx-5\) là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
0
28 tháng 10 2023
\(f'\left(x\right)=\left(sin^2x\right)'+4\cdot\left(sinx'\right)-5'\)
\(=2\cdot sinx\cdot cosx+4\cdot cosx=2cosx\left(sinx+2\right)\)
\(f'\left(x\right)=0\)
=>\(cosx\left(sinx+2\right)=0\)
=>\(cosx=0\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
mà \(x\in\left[0;\dfrac{\Omega}{2}\right]\)
nên \(x=\dfrac{\Omega}{2}\)
\(f\left(\dfrac{\Omega}{2}\right)=sin^2\left(\dfrac{\Omega}{2}\right)+4\cdot sin\left(\dfrac{\Omega}{2}\right)-5\)
=1+4-5=0
\(f\left(0\right)=sin^20+4\cdot sin0-5=-5\)
=>Chọn D
PT
1
CM
7 tháng 6 2018
Ta có : y = sin2x – 4sinx – 5= (sinx- 2)2 - 9
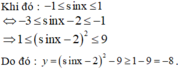
Vậy giá trị nhỏ nhất của hàm số là - 8
Đáp án B
PT
1
PT
1
CM
17 tháng 3 2019
Do đó giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số đã cho là 4 2 - 1 và 7
Đáp án D
CM
25 tháng 3 2019
Chọn C.
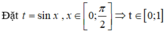
Khi đó, bài toán trở thành tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
trên đoạn [0;1]
CM
26 tháng 8 2018
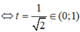
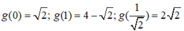
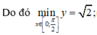
Đáp án B
Ta có y = 4 sin x − 3 cos x = 5 4 5 sinx − 3 5 cos x = 5 sin x − α với sin α = 3 5 cos α = 4 5
Ta có − 1 ≤ sin x − α ≤ 1 ⇒ − 5 ≤ 5 sin x − α ≤ 5 ⇒ M = 5 m = − 5
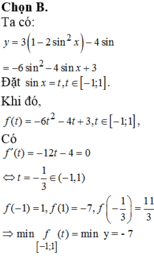
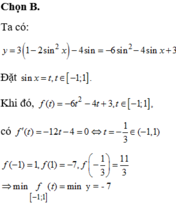
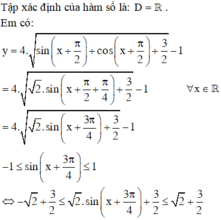
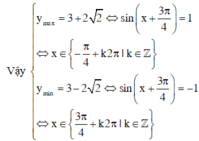
\(y=\left(sinx+1\right)\left(sinx-5\right)\)
Do \(-1\le sinx\le1\Rightarrow\left\{{}\begin{matrix}sinx+1\ge0\\sinx-5< 0\end{matrix}\right.\)
\(\Rightarrow y\le0\Rightarrow y_{max}=0\) khi \(sinx=-1\)
\(y=sin^2x-4sinx+3-8=\left(1-sinx\right)\left(3-sinx\right)-8\)
Do \(-1\le sinx\le1\Rightarrow\left\{{}\begin{matrix}1-sinx\ge0\\3-sinx>0\end{matrix}\right.\) \(\Rightarrow\left(1-sinx\right)\left(3-sinx\right)\ge0\)
\(\Rightarrow y_{min}=-8\) khi \(sinx=1\)
Cưa cưa em hỏi ké phát, phương pháp chung của những dạng tìm gtnn,ln của hàm số lượng giác là biến đổi nó về dạng gì ạ? Và help me with question, pls:
Max: \(\sin^2x+\cos2x+\sin2x\)