Cho F=1-x-\(x^2\)
tìm giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 10 2021
Dễ thấy: \(f\left(x\right)=\left(x+m-1\right)^2-m^2+5m-6\ge-m^2+5m-6\)
Giá trị nhỏ nhất của f(x) đạt lớn nhất tức \(-m^2+5m-6\) đạt lớn nhất
Mà \(g\left(m\right)=-m^2+5m-6=-\left(m-\dfrac{5}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
g(m) đạt lớn nhất khi m=5/2
m cần tìm là 5/2
CM
18 tháng 4 2019
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
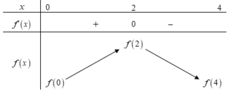
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
17 tháng 2 2019
Bài 1:
a) Ta có: 2x + 2x+3 = 144
2x.(1+23) = 144
2x.9 = 144
2x = 16
x = 4
RR
16 tháng 5 2018
Ta có : \(f\left(x\right)=x^2+6x+15=\left(x+3\right)^2+6\ge6\)
Vậy Min = 6 <=> x = - 3
Nhận thấy , giá trị của x càng tăng thì giá trị của f(x) cũng tăng theo
Vậy f(x) không có giá trị lớn nhất .
16 tháng 5 2018
Có: \(f\left(x\right)=x^2+6x+15=x^2+2.3x+3^2+6=\left(x+3\right)^2+6\)
Có: \(\left(x+3\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+3\right)^2+6\ge6\forall x\)
\(\Rightarrow\)GTNN của f(x) là 6 khi: ( x+3 )2 = 0
x+3 = 0
x=-3
Vậy GTNN của f(x) là 6 khi x=-3
Chúc bạn học tốt!
CD
1
20 tháng 9 2021
Ta có: F = |x - (1 + 1/2)| + |x - 3,5| = |x - 1,5| + |3,5 - x| \(\ge\)|x - 1,5 + 3,5 - x| = 2
Dấu "=" xảy ra<=> (x - 1,5)(3,5 - x) \(\ge\)0 <=> 1,5 \(\le\)x \(\le\)3,5
Vậy MaxF = 2 <=> 1,5 \(\le\)x \(\le\)3,5
8 tháng 4 2023
1:
a: \(A=2+3\sqrt{x^2+1}>=3\cdot1+2=5\)
Dấu = xảy ra khi x=0
b: \(B=\sqrt{x+8}-7>=-7\)
Dấu = xảy ra khi x=-8
TA CÓ ; F=1-X-X^2=-(X^2+2.X.1/2+1/4)+5/4=-(X-1/2)^2+5/4=<5/4
Vậy GTLN của F là 5/4 xảy ra khi x=1/2
\(F=1-x-x^2\)
\(F=\left(-x^2-x-\frac{1}{4}\right)+\frac{5}{4}\)
\(F=-\left[x^2+2\cdot\frac{1}{2}x+\left(\frac{1}{2}\right)^2\right]+\frac{5}{4}\)
\(F=-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(-\left(x+\frac{1}{2}\right)^2\le0\forall x\Rightarrow-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\le\frac{5}{4}\)
Dấu " = " xảy ra <=> x + 1/2 = 0 => x = -1/2
=> MaxF = 5/4 <=> x = -1/2