đặt vào hai đầu đoạn mạch một hiệu điện thế U=36V thì dòng điện chạy qua mạch có cường độ I = 4A . Người ta làm giảm cường độ dòng điện xuống còn 1,5A bằng cách nối thêm vào mạch một điện trở Rx có giá trị bằng bao nhiêu?
# mik cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2021
a,\(=>I=\dfrac{U}{R}=\dfrac{36}{100}=0,36A\)
b,gọi phần R2 là x(ôm)=>R1 là 100-x(ôm)
R1//R2 \(=>1,5=\dfrac{U}{R12}=>1,5=\dfrac{36}{\dfrac{R1R2}{R1+R2}}=\dfrac{36}{\dfrac{x\left(100-x\right)}{x+100-x}}=>x=R2=40\left(om\right)=>R1=60\left(om\right)\)
VT
8 tháng 2 2019
Chọn D. Điện trở R tỉ lệ thuận với hiệu điện thế U và tỉ lệ nghịch với cường độ dòng điện I chạy qua đoạn mạch
VT
24 tháng 9 2017
Đáp án D
Ta có: R = δ l S
Ban đầu: I = U R 0 ( R 0 là điện trở ban đầu của dây)
Khi cắt đôi dây thì chiều dài giảm một nửa → R giảm một nửa → R = R 0 2
Khi mắc song song thì R / / = R 0 4 → Cường độ trong mạch I / / = U R / / = 4 U R 0 = 4 I
Vậy cường độ chạy qua mỗi nửa đoạn dây là I = I / / 2 = 2 I
25 tháng 8 2016
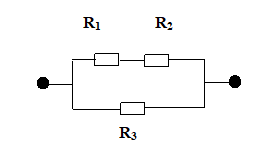
a.Cường độ dòng điện qua mạch: \(I_{mạch}=I_2=\frac{U_2}{R_2}=1,5\left(A\right)\) Hiệu điện thế U: \(U=R_{tđ}\times I_{mạch}=\left(R_1+R_2\right)\times I_{mạch}=60\times1,5=30\left(V\right)\)
b.\(I'=I:2=0,75\left(A\right)\)
\(R_{tđ}=\frac{U}{I'}=\frac{60}{0,75}=80\left(\Omega\right)\)
\(R_3=R_{tđ}-\left(R_1+R_2\right)=80-60=20\left(\Omega\right)\)
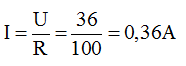
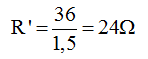
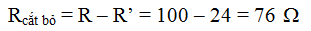
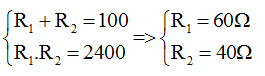
giải
cường độ dòng điện tỉ lệ thuận với hiệu điện thế
có: \(\frac{U1}{U2}=\frac{I1}{I2}\Leftrightarrow\frac{36}{U2}=\frac{4}{1,5}\)
\(\Rightarrow U2=13,5\left(V\right)\)
điện trở \(R_x\) là:
\(I2=\frac{U2}{R_x}\Rightarrow R_x=\frac{U2}{I2}=\frac{13,5}{1,5}=9\left(\Omega\right)\)