Tìm x
Ix - 5/3I < 1/3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
11 tháng 2 2017
a ) 2|x - 3| - 5 = 3 <=> 2|x - 3| = 8 <=> |x - 3| = 4 => x - 3 = ± 4
TH1 : x - 3 = 4 => x = 7
TH2 : x - 3 = - 4 => x = - 1
Vậy x = { - 1; 7 }
b ) 2|2x + 3| + |2x + 3| = 6 <=> 3|2x + 3| = 6 => |2x + 3| = 2 => 2x + 3 = ± 2
=> x = { - 5/2 ; - 1/2 }
c ) 3|x + 1|2 + |x + 1|2 = 16
4|x + 1|2 = 16
=> |x + 1|2 = 4 = 22 ( ko xét TH |x + 1| = - 2 vì |x + 1| ≥ 0 )
=> |x + 1| = 2 => x + 1 = ± 2 => x = { - 3; 1 }
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2021
\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
CM
24 tháng 10 2018
Chọn đáp án A
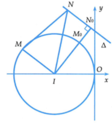
Giả sử z 1 = x 1 + y 1 i có điểm biểu diễn là M x 1 ; y 1 và z 2 = x 2 + y 2 i có điểm biểu diễn là N x 2 ; y 2
Từ giả thiết ta có
Suy ra tập hợp các điểm M là đường tròn (C): x + 5 2 + y 2 = 25
Suy ra tập hợp các điểm N là đường thẳng d: 8x +6y -35 = 0
Ta thấy đường thẳng d không cắt đường tròn (C) và z 1 - z 2 = M N
Áp dụng bất đẳng thức tam giác cho bộ ba điểm (I ,M, N) ta có
với N 0 là hình chiếu của I trên d
Khi đó
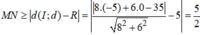
Dấu “=” xảy ra khi và chỉ khi N ≡ N 0 và M ≡ M 0 , với M 0 là giao điểm của đoạn thẳng I N 0 với đường tròn (C).
26 tháng 1 2015
4. A=7-x/x-5=(-(x-5)+2)/x-5=-1+2/x-5
A nhỏ nhất khi 2/x-5 nhỏ nhất.mà 2/x-5 nho nhất khi x-5 lớn nhất(a)
TH1: x-5>0=>x>5=>2/x-5>0(1)
Th2:x-5<0=>x<5=>2/x-5<0(2)
(1), (2)=>x-5<0(b)
(a),(b)=>x-5=-1=>x=4
vậy A nhỏ nhất là -3
CM
30 tháng 11 2018
Chọn A.
Ta có: z = z1 + z2 = (-2 + 3i) + (5 + 3i) = (-2 + 5) + (3 + 3)i = 3 + 6i
Bài làm:
Ta có: \(\left|x-\frac{5}{3}\right|< \frac{1}{3}\)
\(\Leftrightarrow-\frac{1}{3}< x-\frac{5}{3}< \frac{1}{3}\)
\(\Leftrightarrow\frac{4}{3}< x< 2\)