Tìm m để y = 2x3 - mx2 + 2x đồng biến trên (-2,0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.
.
.
CM
17 tháng 8 2018
Đáp án A
Hàm số đồng biến trên 
.
Xét hàm số 
.
Khi đó 
.
Bảng biến thiên:
Từ bảng biến thiên suy ra các giá trị cần tìm của m là 
.
CM
19 tháng 5 2017
Đáp án A
T X D : D = ℝ \ 1
Ta có: y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 = m x − 2 + m 2 − 2 m x − 1 ⇒ y ' = m − m 2 − 2 m x − 1 2
hàm số luôn đồng biến trên tập xác định của nó khi y ' ≥ 0 ∀ x ∈ D (dấu bằng xảy ra tại hữu hạn điểm)
⇔ m − m 2 − 2 m x − 1 2 ≥ 0 ∀ x ∈ D ⇔ x x − 1 2 ≥ m 2 − 2 m ∀ x ∈ D
Với m = 0 ⇒ y ' = 0 ∀ x ∈ D (không thỏa mãn dấu bằng xảy ra tại hữu hạn điểm)
Khi đó hàm số luôn đồng biến trên tập xác định m > 0 m 2 − 2 m ≤ 0 ⇔ 0 < m ≤ 2
AH
Akai Haruma
Giáo viên
2 tháng 12 2023
Lời giải:
a. $y=mx-x^2-2x+mx^2+m=x^2(m-1)+x(m-2)+m$
Lấy $x_1,x_2\in R$ sao cho $x_1\neq x_2$
$y(x_1)=x_1^2(m-1)+x_1(m-2)+m$
$y(x_2)=x_2^2(m-1)+x_2(m-2)+m$
Để hàm đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{x_1^2(m-1)+x_1(m-2)+m-[x_2^2(m-1)+x_2(m-2)+m]}{x_1-x_2}>0$
$\Leftrightarrow \frac{(m-1)(x_1^2-x_2^2)+(m-2)(x_1-x_2)}{x_1-x_2}>0$
$\Leftrightarrow (m-1)(x_1+x_2)+(m-2)>0$
Với mọi $x_1,x_2\in\mathbb{R}$ thì không có cơ sở để tìm $m$ sao cho hàm đồng biến.
b.
Xét tương tự câu 1, với $x_1\neq x_2\in \mathbb{R}$ thì hàm đồng biến khi:
$(m^2-3m+2)(x_1+x_2)+(m-1)>0$
Với mọi $x_1, x_2\in\mathbb{R}$ thì điều này xảy ra khi:
$m^2-3m+2=0$ và $m-1>0$
$\Leftrightarrow (m-1)(m-2)=0$ và $m-1>0$
$\Leftrightarrow m=2$
CM
4 tháng 12 2019
Tập xác định: D = R ∖ { 1 }
· y ' = m x 2 + 2 m x + 1 x + 1 2
· Hàm số luôn đồng biến trên từng khoảng xác định của nó khi và chỉ khi y ' > 0; ∀ x ≠ 1
· Xét m = 0, ta có y ' = 1 x + 1 2 > 0 ; ∀ x ≠ 1 (tm).
· Xét m ≠ 0 .Yêu cầu bài toán
⇔ ∆ ' = m 2 - m ≤ 0 m > 0 ⇔ 0 ≤ m ≤ 1 m > 0 ⇔ 0 < m ≤ 1
Kết luận: 0 ≤ m ≤ 1
Đáp án B
CM
25 tháng 3 2019
Đáp án B
Ta có y ' = − 3 x 2 + 2 m x . Hàm số đồng biến trên khoảng 0 ; 2 ⇔ y ' ≥ 0 , ∀ x ∈ 0 ; 2 ⇒ − 3 x 2 + 2 m x ≥ 0 ⇔ m ≥ 3 x 2 , x ∈ 0 ; 2
Xét hàm số f x = 3 x 2 , x ∈ 0 ; 2 ⇒ f ' x = 3 2 > 0 ⇒ f x đồng biến trên đoạn 0 ; 2 .
Suy ra f x 0 ; 2 < f 2 = 3 ⇒ m ≥ 3.
CM
10 tháng 3 2019
Đáp án B
Ta có y ' = 3 x 2 + 2 m x + 1 − 2 m
Hàm số đồng biến trên − 3 ; 0 ⇔ y ' ≥ 0 , ∀ x ∈ − 3 ; 0 ⇔ 3 x 2 + 2 m x + 1 − 2 m ≥ 0 , ∀ x ∈ − 3 ; 0
⇔ m 2 x − 2 ≥ − 3 x 2 − 1 ⇔ m ≤ − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 1
Xét hàm số
f x = − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 ⇒ f ' x = − 6 x 2 + 12 x + 2 2 x − 2 2 ⇒ f ' x = 0 ⇔ x = 3 ± 2 3 3
Ta có bảng biến thiên hàm số f x như sau:
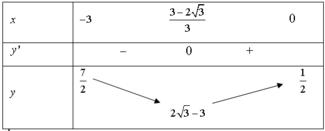
Suy ra f x − 3 ; 0 ≥ 2 3 − 3 ⇒ 1 ⇔ m ≤ 2 3 − 3
CM
22 tháng 9 2019
Đáp án D
Ta có: y ' = x 2 − 2 m x + 4 m − 3 . Để hàm số đồng biến trên R thì y ' ≥ 0 ∀ x ∈ ℝ
⇔ Δ ' = m 2 − 4 m + 3 ≤ 0 ⇔ 1 ≤ m ≤ 3 ⇒ m lớn nhất bằng 3
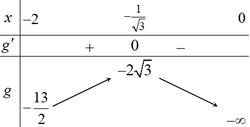
\(y'=f\left(x\right)=6x^2-2mx+2\) (1)
Để hàm số đồng biến trên \(\left(-2;0\right)\Leftrightarrow f\left(x\right)\ge0\) ; \(\forall x\in\left(-2;0\right)\)
\(\Leftrightarrow6x^2+2\ge2mx\Leftrightarrow\frac{3x^2+1}{x}\le m\Leftrightarrow m\ge\max\limits_{\left(-2;0\right)}\frac{3x^2+1}{x}\)
Xét \(g\left(x\right)=\frac{3x^2+1}{x}\Rightarrow g'\left(x\right)=\frac{3x^2-1}{x^2}=0\Rightarrow x=-\frac{1}{\sqrt{3}}\)
Từ BBT ta thấy \(\max\limits_{\left(-2;0\right)}g\left(x\right)=g\left(-\frac{1}{\sqrt{3}}\right)=-2\sqrt{3}\)
\(\Rightarrow m\ge-2\sqrt{3}\)
vì sao chỗ biến đổi lại đổi dấu thành m> hoặc = vậy ạ