Tính giá trị của hàm số y = arctg(1+x/1-x)-arctgx với x khác 1 (đây là đề)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(F'_x=\frac{1}{\pi\left(1+x^2\right)}\left(\frac{1}{\pi}arctgy+\frac{1}{2}\right)\) \(\forall x,y\)
\(\Rightarrow F"_{xy}=\frac{1}{\pi\left(1+x^2\right)}.\frac{1}{\pi\left(1+y^2\right)}=\frac{1}{\pi^2\left(1+x^2+y^2+x^2y^2\right)}\)
\(\Rightarrow\)Hàm mật độ của BNN hai chiều (X, Y) là
\(f\left(x,y\right)=\frac{1}{\pi^2\left(1+x^2+y^2+x^2y^2\right)}\)

Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
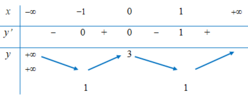
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

1.Đại lượng y là hàm số của đại lượng x vì ta có mỗi giá trị của đại lượng x đều có một giá trị tương ứng của đại lượng y . Giá trị tương ứng ấy của đại lượng y là duy nhất.
2. Đại lượng y không phải là hàm số của đại lượng x vì ứng với giá trị x = 5 chẳng hạn ta có hai giá trị của y (ước tự nhiên của 5 là 1 và 5)
3. Dựa vào định nghĩa các phép toán về số hữu tỉ. Chú ý rằng với các số hữu tỉ thì kết quả của các phép toán này là số hữu tỉ. Chẳng hạn câu b). Giả sử tích của số hữu tỉ \(x\ne0\)với số vô tỉ y là số hữu tỉ z. Ta có x.y=z.
Như vậy thì \(y=\frac{z}{x}\). Nhưng z và x \(\left(x\ne0\right)\)là hai số hữu tỉ nên thương của chúng cũng là số hữu tỉ. Suy ra y là số hữu tỉ, trái với đề bài. Vậy tích của một số hữu tỉ khác 0 với một số vô tỉ là một số vô tỉ.

Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.

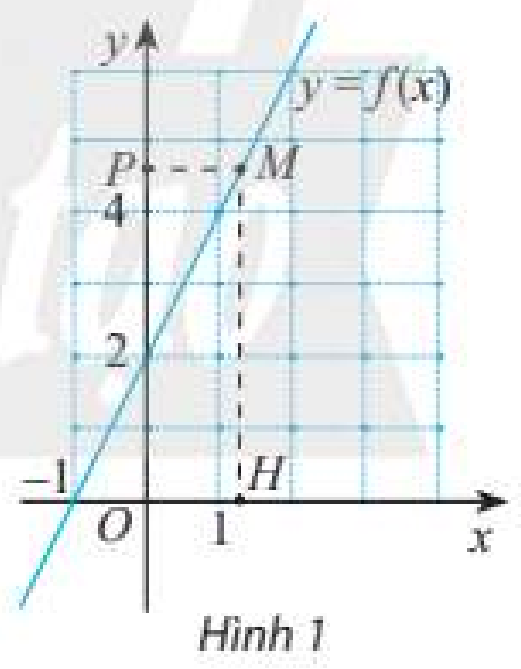
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).

\(y'=\frac{\left(\frac{x+1}{-x+1}\right)}{1+\left(\frac{x+1}{-x+1}\right)^2}-\frac{1}{1+x^2}=\frac{2}{\left(1-x\right)^2}.\frac{\left(1-x\right)^2}{\left(1-x\right)^2+\left(x+1\right)^2}-\frac{1}{1+x^2}\)\(=\frac{2}{2\left(1+x^2\right)}-\frac{1}{1+x^2}=0;\forall x\ne1\)
- Xét \(x\in\left(-\infty,1\right):y'=0,\forall x\in\left(-\infty,1\right)\)nên y là hằng số trên \(\left(-\infty,1\right)\)
mà \(y\left(0\right)=arctg1-arctg0=\frac{\eta}{4}-0=\frac{\eta}{4}\Rightarrow y=\frac{\eta}{4},\forall x\in\left(-\infty,1\right)\)(n số pi ở đây không chắc là đúng chưa mình mở vô hộp có kí tự số pi rồi mà thấy kí tự có hơi lạ lạ, thông cảm nhá)
- Xét \(x\in\left(1,\infty\right):y'=0,\forall x\in\left(1,\infty\right)\)
\(\Rightarrow y\)là hằng số trên \(\left(1,\infty\right)\)
\(\Rightarrow arctg\left(\frac{1+x}{1-x}\right)-arctgx=k,\forall x\in\left(1,\infty\right)\)
Cho \(x\rightarrow\infty\)thì \(\left(\frac{1+x}{1-x}\right)\rightarrow-1:arctg\left(-1\right)-\frac{\eta}{2}=k\Rightarrow k=-\frac{\eta}{4}-\frac{\eta}{2}=-\frac{3\eta}{4}\)
Do đó \(y=-\frac{3\eta}{4},\forall x\in\left(1,\infty\right).\)
Vậy \(y=\hept{\begin{cases}\frac{\eta}{4}\left(neux< 1\right)\\-\frac{3\eta}{4}\left(neux>1\right)\end{cases}}\)nếu đó nha.