Question

[Não Não]

Bình thông nhau gồm 2 nhánh hình trụ tiết diện lần lượt là S1 và S2 chứa nước. Trên mặt nước có đặt các pitton mỏng, khối lượng m1 và m2. Mực nước ở pitton 1 cao hơn pitton 2 một đoạn h.

a. Tìm khối lượng m của quả cân đặt lên pitton lớn để mực nước hai bên bằng nhau.

b. Nếu đặt quả cân trên sang pitton nhỏ thì mực nước bây giờ ở hai nhanh chênh lệch nhau một đoạn h' bằng bao nhiêu?

Answer 1

[ling Giang nguyễn]

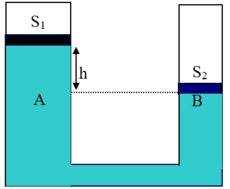
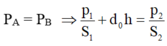
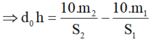
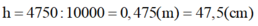
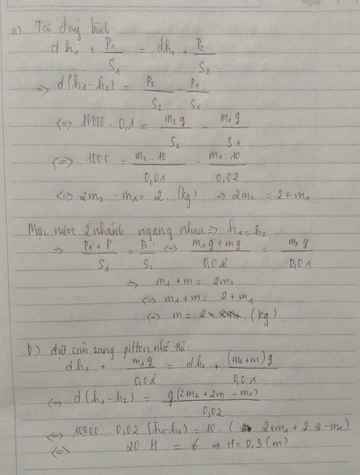
a. Gọi A và B là 2 điểm nằm trên cùng 1 mặt phẳng ngang như hình vẽ:

Trọng lượng của 2 pittong là:

\(P_1=10m_1=F_1\)

\(P_2=10m_2=F_2\)

Khi chưa đặt qủa cân thì: pA=pB

Hay \(\frac{F_1}{S_1}+d_0h=\frac{F_2}{S_2}\)

\(\Leftrightarrow\frac{10m_1}{S_1}+10D_0h=\frac{10m_2}{S_2}\)

\(\Rightarrow\frac{m_1}{S_1}+D_0h=\frac{m_2}{S_2}\left(1\right)\)

Khi vật nặng được đặt lên pittong thì :

\(\frac{F_1+P}{S_1}=\frac{F_2}{S_2}\)\(\Rightarrow\frac{m_1+m}{S_1}=\frac{m_2}{S_2}\left(2\right)\)

Trừ (1), (2), vế theo vế ta có:

\(\frac{m_1}{S_1}+D_0h-\frac{m_1}{S_1}-\frac{m}{S_1}=\frac{m_2}{S_2}-\frac{m_2}{S_2}\)

\(\Leftrightarrow D_0h=\frac{m}{S_1}\)\(\Rightarrow m=D_0S_1h\)

b,

Gọi H là chênh lệch mực nước ở 2 nhánh khi đặt quả cân sang pittong nhỏ.

Nếu đặt quả cân sang pittong nhỏ thì

\(\frac{F_1}{S_1}+dH=\frac{F_2+P}{S_2}\)\(\Rightarrow\frac{m_1}{S_1}+D_0H=\frac{m_2+m}{S_2}\left(3\right)\)

Trừ (1), (3) vế theo vế, ta có:

\(\frac{m_1}{S_1}+D_oh-\frac{m_1}{S_{ }}-D_0H=\frac{m_2}{S_2}-\frac{m_2}{S_2}-\frac{m}{S_2}\)

\(\Rightarrow D_0h-D_0H=-\frac{m}{S_2}\)

\(\Leftrightarrow D_0\left(H-h\right)=\frac{D_0S_1h}{S_2}\)

\(\Leftrightarrow H-h=\frac{S_1h}{S_2}\)\(\Rightarrow H=\left(1+\frac{S_1}{S_2}\right)h\)