CHO ABCD LÀ HCH AD<AB.CÓ DH LÀ ĐƯỜNG CAO TẠI AC H€AC, CÓ AE LÀ TPG CỦA GÓC DAC.K LÀ GIAO ĐIỂM CỦA AE VÀ DH.
CM HỆ THỨC : AC.DK=CE.DA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

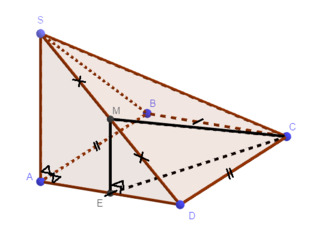
Gọi E là trung điểm AD, ta có: ME//SA (ME là đường trung bình tam giác SAD) và SA, CE chéo nhau; suy ra (MCE) vuông góc (ABCD) và không chứa SA; suy ra SA//(MCE). Suy ra, d(SA,CM) = d(SA,(MCE)) = d(A,(MCE)) = d(D,(MCE)) = d(D,EC) = ED.DC/EC = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
Xin lỗi, mình sửa lại bài giải.
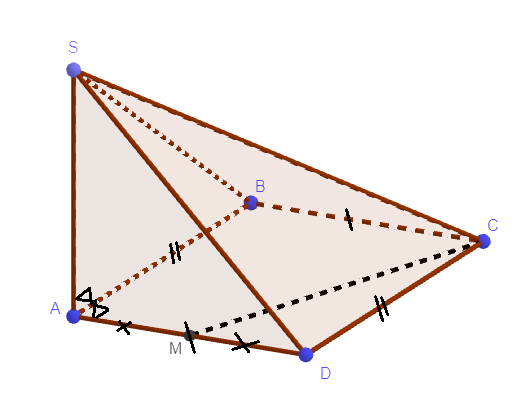
d(SA,CM) = d(A,CM) = d(D,CM) = MD.DC/CM = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.

, - Hình thoi có 2 đừờng chéo vuông góc với nhau nên góc BOC = 90 độ (1)
- BI // AC và CI // Bo ==> OBIC là Hình bình hành(2)
từ 1 và 2 suy ra OBIC là Hình chữ nhật
b,
- ABCD là hình thoi nên AB=BC=CD=DA (3)
- OBIC là HCN nên 2 dg chéo OI=BC (4)
từ 3 và 4 suy ra AB=OI
c,
đieu kiên bài cho <=> OB=OC <=> ABCD là hình vuông.