Cho một hình tam giác ABC có s= 180 cm2.Trên cạnh CA và CB lần lượt lấy 2 điểm M và N sao cho CM=1/3 CA,CN=2/3 CB.Tính tỉ số diện tich giữa tứ giác ANMB và tam giác ABC?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
13 tháng 7 2020
Xét tam giác BMC và tam giác BCA có chung chiều cao hạ từ B xuống AC, đáy CM = 1/3 đáy CA
=> \(S_{BMC}=\frac{1}{3}.S_{BCA}=\frac{1}{3}.180=60\left(cm^2\right)\)
Xét tam giác BMC và tam giác NMC có chung chiều cao hạ từ đỉnh M xuống cạnh BC, đáy CN = 2/3 đáy CB
\(\Rightarrow S_{NMC}=\frac{2}{3}.S_{BMC}=\frac{2}{3}.60=40\left(cm^2\right)\)
\(\Rightarrow S_{AMNB}=S_{ABC}-S_{MNC}=180-40=140\left(cm^2\right)\)
=> Tỉ số giữa \(\frac{S_{AMNB}}{S_{ABC}}=\frac{140}{180}=\frac{7}{9}\)
Vậy tỉ số diện tích giữa tứ giác AMNB và tam giác ABC là 7/9
25 tháng 6 2023
Cho tui tick nha
Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC
Diện tích tam giác ABN là:
64 x 1/4 = 16 (cm2 )
Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA
Diện tích tam giác BMN là:
16 x 1/2 = 8 (cm2 )
Đáp số: 8 cm2
28 tháng 3 2017
Mình cũng đang gặp bài này, có ai biết bài này kh giải chi tiết ra giùm mình với nhé
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 6 2023
\(\dfrac{CP}{CA}=\dfrac{2}{3}\Rightarrow\dfrac{AP}{CA}=\dfrac{1}{3}\)
Hai tg ABP và tg ABC có chung đường cao từ B->CA nên
\(\dfrac{S_{ABP}}{S_{ABC}}=\dfrac{AP}{CA}=\dfrac{1}{3}\Rightarrow S_{ABP}=\dfrac{1}{3}xS_{ABC}\)
Hai tg AMP và tg ABP có chung đường cao từ P->AB nên
\(\dfrac{S_{AMP}}{S_{ABP}}=\dfrac{AM}{AM}=\dfrac{1}{4}\Rightarrow S_{AMP}=\dfrac{1}{4}xS_{ABP}=\dfrac{1}{4}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{12}xS_{ABC}\)
\(S_{BCP}=S_{ABC}-S_{ABP}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)
\(\dfrac{BN}{BC}=\dfrac{2}{3}\Rightarrow\dfrac{CN}{BC}=\dfrac{1}{3}\)
Hai tg CNP và tg BCP có chung đường cao từ P->BC nên
\(\dfrac{S_{CNP}}{S_{BCP}}=\dfrac{CN}{BC}=\dfrac{1}{3}\Rightarrow S_{CNP}=\dfrac{1}{3}xS_{BCP}=\dfrac{1}{3}x\dfrac{2}{3}xS_{ABC}=\dfrac{2}{9}xS_{ABC}\)
\(\dfrac{AM}{AB}=\dfrac{1}{4}\Rightarrow\dfrac{BM}{AB}=\dfrac{3}{4}\)
Hai tg BCM và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{BCM}}{S_{ABC}}=\dfrac{BM}{AB}=\dfrac{3}{4}\Rightarrow S_{BCM}=\dfrac{3}{4}xS_{ABC}\)
Hai tg BMN và tg BCM có chung đường cao từ M->BC nên
\(\dfrac{S_{BMN}}{S_{BCM}}=\dfrac{BN}{BC}=\dfrac{2}{3}\Rightarrow S_{BMN}=\dfrac{2}{3}xS_{BCM}=\dfrac{2}{3}x\dfrac{3}{4}xS_{ABC}=\dfrac{1}{2}xS_{ABC}\)
\(S_{MNP}=S_{ABC}-S_{AMP}-S_{CNP}-S_{BMN}=\)
\(=S_{ABC}-\dfrac{1}{12}xS_{ABC}-\dfrac{2}{9}xS_{ABC}-\dfrac{1}{2}xS_{ABC}=\)
\(=\dfrac{11}{36}xS_{ABC}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
cô làm rồi em nhé
https://olm.vn/cau-hoi/cho-tam-giac-abc-co-dien-tich-180-cm2-tren-cac-canh-ab-bc-ca-lan-luot-lay-cac-diem-m-n-p-sao-cho-am-23-ab-bn-34-bc-va-cp-13-ca-tinh-di.8088189515587
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
AP = AC - PC = AC - \(\dfrac{1}{3}\)AC = \(\dfrac{2}{3}\)AC
SAMP = \(\dfrac{2}{3}\)SACM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AC và AP = \(\dfrac{2}{3}\)AC)
SACM = \(\dfrac{2}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và AM = \(\dfrac{2}{3}\)AB)
SAMP = \(\dfrac{2}{3}\times\dfrac{2}{3}\)SABC = 180 \(\times\dfrac{4}{9}\) = 80 (cm2)
SBMN = \(\dfrac{3}{4}\)SBCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{3}{4}\)BC)
BM = AB - AM = AB - \(\dfrac{2}{3}\)AB = \(\dfrac{1}{3}\)AB
SBCM = \(\dfrac{1}{3}\)SABC( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{1}{3}\)AB)
SBMN = \(\dfrac{3}{4}\times\dfrac{1}{3}\)SABC = 180 \(\times\dfrac{1}{4}\) = 45 (cm2)
CN = BC - BN = BC - \(\dfrac{3}{4}\)BC = \(\dfrac{1}{4}\)BC
SCPN = \(\dfrac{1}{4}\)SCPB ( vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{4}\)BC)
SCBP = \(\dfrac{1}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và CP = \(\dfrac{1}{3}\)CA)
SCPN = \(\dfrac{1}{4}\times\dfrac{1}{3}\)SABC = 180 \(\times\) \(\dfrac{1}{12}\) = 15 (cm2)
Diện tích tam giác MNPQ là:
180 - ( 80 + 45 + 15) = 40 (cm2)
Đáp số 40 cm2
2 tháng 6 2023
a: S BMC=2/3*90=60cm2
b: S ANC=1/3*90=30cm2
=> S AMN=1/3*30=10cm2
S ABN=2/3*90=60cm2
=>S AMNB=70cm2
6 tháng 7 2016
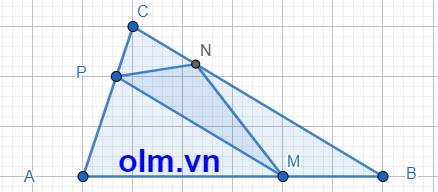
a)Nối K với C
SABN = \(\frac{2}{3}\)SABC vì:
- Đáy BN = \(\frac{2}{3}\)đáy BC
- Chung đường cao từ đỉnh A xuống đáy BC
SANM = \(\frac{1}{3}\)SANC vì:
Đáy AM = \(\frac{1}{3}\)đáy AC
- Chung đường cao từ đỉnh N xuống đáy AC
SABN là:
180 : 3 x 2 = 120 (cm2)
SANC là:
180 - 120 = 60 (cm2)
SANM là:
60 : 3 = 20 (cm2)
Mà SAMNB = SABN + SANM
Vậy SAMNB là:
120 + 20 = 140 (cm2)
b) SBKN = \(\frac{2}{1}\)SNKC vì:
- Đáy BN = \(\frac{2}{1}\)đáy NC
- Chung đường cao từ đỉnh K xuống đáy BC
Mà hai tam giác này còn chung đáy KN, suy ra đường cao từ đỉnh B xuống đáy KN = \(\frac{2}{1}\)đường cao từ đỉnh C xuống đáy KN
Hai đường cao này lần lượt là đường cao của hai tam giác ABK và ACK, => SABK = \(\frac{2}{1}\)SACK
- SAMK = \(\frac{1}{3}\)SACK vì:
- Đáy AM = \(\frac{1}{3}\)đáy AC
- Chung đường cao từ đỉnh K xuống đáy AC
Ta có:
SACK = \(\frac{1}{2}\)SABK
SAMK = \(\frac{1}{3}\)SACK
=> SAMK = \(\frac{1}{3}\)x \(\frac{1}{2}=\frac{1}{6}\)SABK
SABM = \(\frac{1}{3}\)SABC vì:
- Đáy AM = \(\frac{1}{3}\)đáy AC
- Chung đường cao từ đỉnh B xuống đáy AC
S ABM là:
180 : 3 = 60 (cm2)
Ta có:
SABM = SAMK + SABK
Vậy coi SAMK là 1 phần thì SABK là 6 phần như thế, SABM là : 6 + 1 = 7 (phần như vậy)
S ABK là:
60 : 7 x 6 = \(\frac{360}{7}\)(cm2)
Đáp số: a) 140cm2
b) \(\frac{360}{7}\)cm2