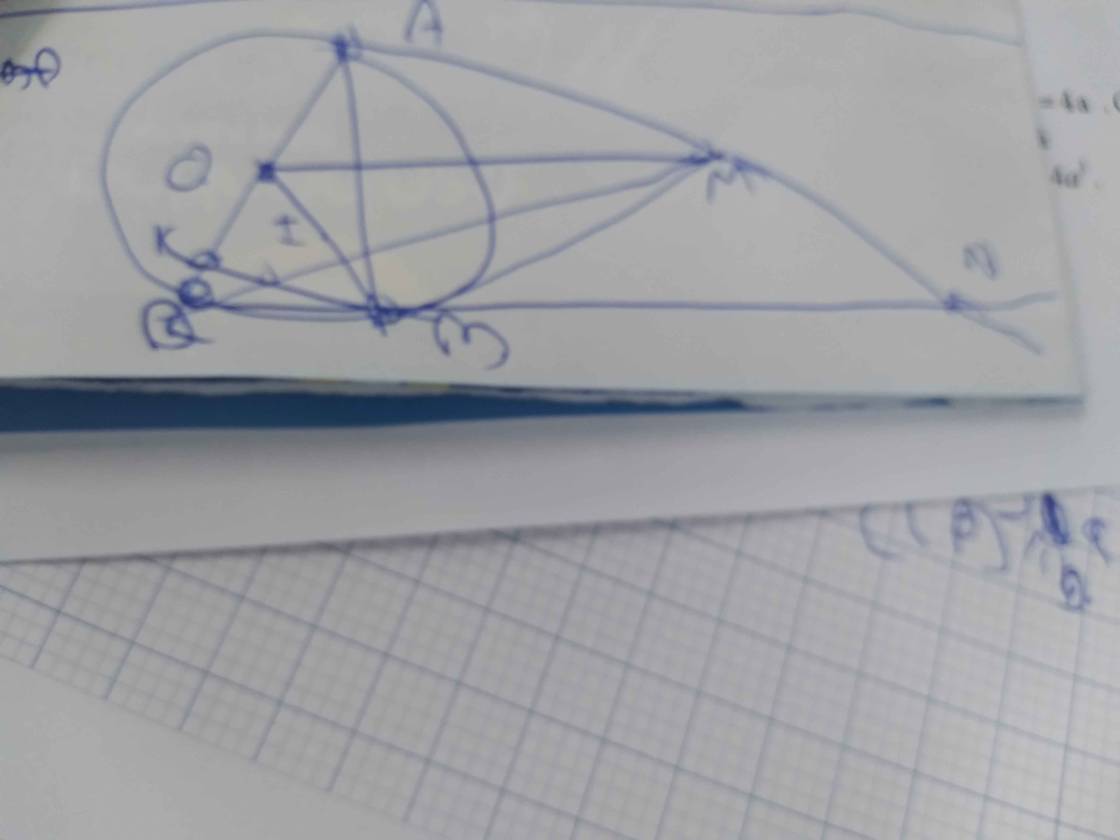
Cho đường tròn(o,r) từ một điểm A trên (o). trên đường thẳng d lấy điểm M bất kì (M khác A ) kẻ các tuyến MNP và gọi K Là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). kẻ AC vuông góc với MB ,BP vuông góc với MA gọi H là giao điểm của AC và AB ,I là giao điểm của OM và AB ,I là giao điểm của OM và AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 12 2023
a: ΔONP cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)NP tại K
Ta có: \(\widehat{OAM}=\widehat{OBM}=\widehat{OKM}=90^0\)
=>O,A,M,B,K cùng thuộc đường tròn đường kính OM
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot OM=OA^2=R^2\)
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot IM=IA^2\)
c: AC\(\perp\)BM
OB\(\perp\)BM
Do đó: OB//AC
=>OB//AH
BD\(\perp\)MA
OA\(\perp\)MA
Do đó: BD//OA
=>BH//OA
Xét tứ giác OBHA có
OB//HA
OA//HB
Do đó: OBHA là hình bình hành
Hình bình hành OBHA có OB=OA
nên OBHA là hình thoi
d: OBHA là hình thoi
=>OH là đường trung trực của BA
mà M nằm trên đường trung trực của BA(cmt)
nên O,H,M thẳng hàng
22 tháng 10 2023
1: Xét tứ giác AMBO có
\(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
=>AMBO là tứ giác nội tiếp đường tròn đường kính OM
2: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
\(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)
=>O,K,A,M,B cùng thuộc 1 đường tròn
CM
4 tháng 7 2018
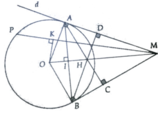
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng
14 tháng 12 2021
1 vì K là trung điểm NP nên OK vuông góc NP ( Quan hệ đường kính và dây cung ) suy ra góc OKM=90 độ .Theo tính chất tiếp tuyến ta có góc OAM=90 độ , góc OBM = 90 độ như vậy K,A,B cùng nhìn OM dưới một góc 90 độ nên cùng nằm trên dường tròn đường kính OM . vậy ..........
27 tháng 12 2021
a: Xét tứ giác MBOC có
\(\widehat{MBO}+\widehat{MCO}=180^0\)
Do đó: MBOC là tứ giác nội tiếp
18 tháng 12 2023
a: Xét tứ giác OBMA có \(\widehat{OBM}+\widehat{OAM}=90^0+90^0=180^0\)
nên OBMA là tứ giác nội tiếp
=>O,B,M,A cùng thuộc một đường tròn
b: Ta có: ΔOBC cân tại O
mà OM là đường cao
nên OM là phân giác của góc BOC
Xét ΔOBM và ΔOCM có
OB=OC
\(\widehat{BOM}=\widehat{COM}\)
OM chung
Do đó: ΔOBM=ΔOCM
=>\(\widehat{OBM}=\widehat{OCM}\)
mà \(\widehat{OBM}=90^0\)
nên \(\widehat{OCM}=90^0\)
=>MC là tiếp tuyến của (O)
KV
18 tháng 12 2023
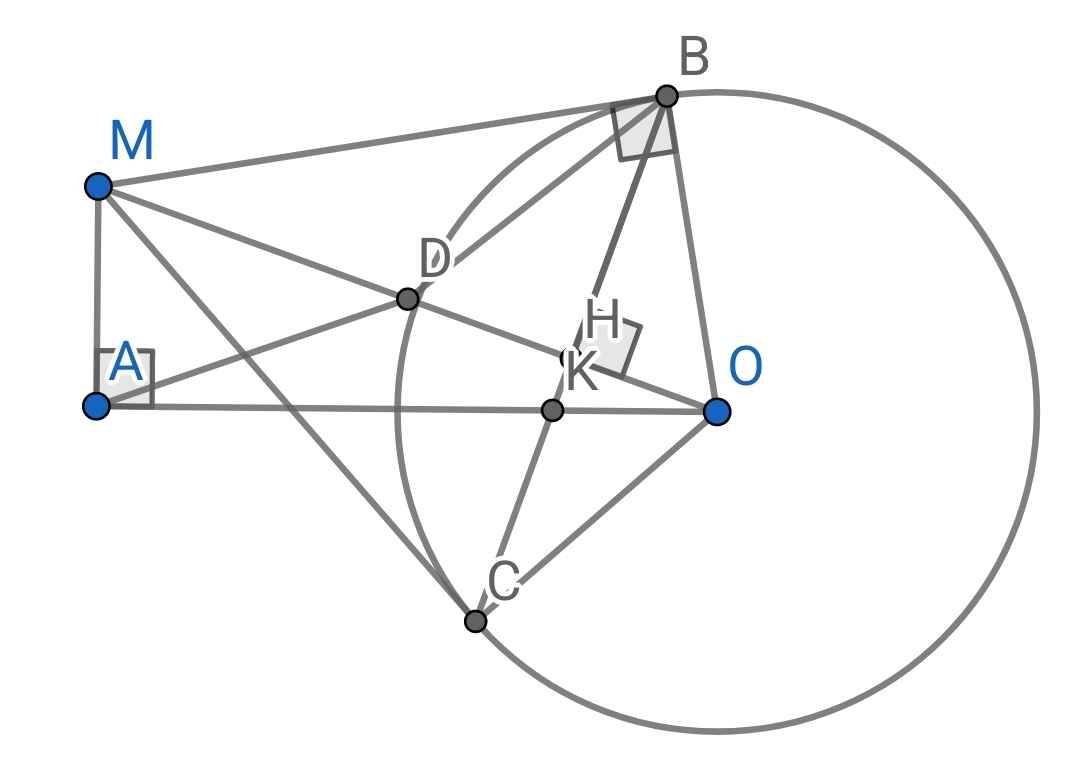a) Gọi D là trung điểm của MO
∆OAM vuông tại A có AD là đường trung tuyến ứng với cạnh huyền OM
⇒ AD = OD = MD = OM : 2 (1)
∆OBM vuông tại B có BD là đường trung tuyến ứng với cạnh huyền OM
⇒ BD = OD = MD = OM : 2 (2)
Từ (1) và (2) ⇒ AD = BD = OD = MD
Vậy A, B, O, M cùng thuộc (D, AD)
b) Xét hai tam giác vuông: ∆OHB và ∆OHC có:
OH là cạnh chung
OB = OC = bán kính
⇒ ∆OHB = ∆OHC (cạnh huyền - cạnh góc vuông)
⇒ ∠HOB = ∠HOC (hai góc tương ứng)
⇒ ∠MOB = ∠MOC
Xét ∆MOB và ∆MOC có:
OM là cạnh chung
∠MOB = ∠MOC (cmt)
OB = OC = bán kính)
⇒ ∆MOB = ∆MOC (c-g-c)
⇒ ∠OBM = ∠OCM (hai góc tương ứng)
⇒ ∠OCM = 90⁰
⇒ MC ⊥ OC
Mà OC là bán kính của (O)
⇒ MC là tiếp tuyến của (O)