Cho 3 số nguyên dương a,b,c .Gọi x là tích của 3 số a,b,c.Hỏi trong cách viết số x thành lũy thừa bậc n của một số nguyên thì n lớn nhất là bao nhiêu.
Ai biết giúp mình đi.Cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BA
21 tháng 11 2023
import math
# Nhập 3 số nguyên x, y, z
x = int(input("Nhập số nguyên x: "))
y = int(input("Nhập số nguyên y: "))
z = int(input("Nhập số nguyên z: "))
# Tính tích a của x, y, z
a = x * y * z
# Tìm số mũ lớn nhất n sao cho a có thể viết dưới dạng lũy thừa bậc n của một số nguyên dương
n = int(math.log2(a))
print("Số mũ lớn nhất n mà a có thể viết dưới dạng lũy thừa bậc n của một số nguyên dương là:", n)
Chương trình này sẽ nhận 3 số nguyên từ người dùng, tính tích của chúng, và sau đó tìm số mũ lớn nhất mà tích đó có thể được viết dưới dạng lũy thừa của một số nguyên dương. Chúng tôi sử dụng hàm math.log2 để tính số mũ lớn nhất. Lưu ý rằng kết quả sẽ được làm tròn xuống số nguyên gần nhất.
AH
Akai Haruma
Giáo viên
9 tháng 7 2020
Đề bài thiếu.
Thực sự nếu các bạn không kiểm tra kỹ đề trước khi đăng thì không thể mong mỏi nhiều về việc nhận được sự hỗ trợ từ mọi người cả.
7 tháng 4 2019
Đặt A là số cần tìm. Ta có: A= 5m^5 = 3.n^3 = 2.p^2
Như vậy A có các ước nguyên tố 5,3,2. Mà A là số bé nhất thỏa mãn nên ta có A = 5^a.3^b.2^c
Xét nhân tử 5^a, vì A/3=n^3, A/2=p^2 nên n^3,p^2 chứa nhân tử 5^a=> a phải chia hết cho 2,3
Mặt khác A=5.m^5 nên a chia 5 dư 1 => a nhỏ nhất là 6
Tương tự ta có b chia hết cho 2,5, chia 3 dư 1 nên b nhỏ nhất là 10
c chia hết cho 5,3 chia 2 dư 1 nên c nhỏ nhất là 15
Vậy A nhỏ nhất là 5^6.3^10.2^15. Thử lại thỏa mãn.
CM
3 tháng 12 2019
Đáp án C
Yêu cầu bài toán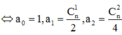 
lập thành cấp số cộng
Khi và chỉ khi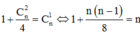 
Do đó, số hạng tổng quát của khai triển là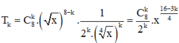 
Số hạng mà lũy thừa của x là số nguyên ứng với 
mà 
Suy ra k = {0;4;8} → Có 3 số hạng lũy thừa của x là số nguyên
14 tháng 8 2023
a: Cho \(a\in R;n\in Z^+\) thì \(a^n=a\cdot a\cdot...\cdot a\)(n chữ số a)
b: \(a^0=1\)
Đặt \(\left(\sqrt[3]{a};\sqrt[3]{b};\sqrt[3]{c}\right)=\left(x^3;y^3;z^3\right)\Rightarrow xyz=1\)
Áp dụng BĐT \(x^3+y^3\ge xy\left(x+y\right)\) ta được:
\(P=\frac{1}{x^3+y^3+1}+\frac{1}{y^3+z^3+1}+\frac{1}{z^3+x^3+1}\)
\(P\le\frac{1}{xy\left(x+y\right)+1}+\frac{1}{yz\left(y+z\right)+1}+\frac{1}{zx\left(z+x\right)+1}\)
\(P\le\frac{xyz}{xy\left(x+y\right)+xyz}+\frac{xyz}{yz\left(y+z\right)+xyz}+\frac{xyz}{zx\left(z+x\right)+xyz}\)
\(P\le\frac{z}{x+y+z}+\frac{x}{x+y+z}+\frac{y}{x+y+z}=1\)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(a=b=c=1\)