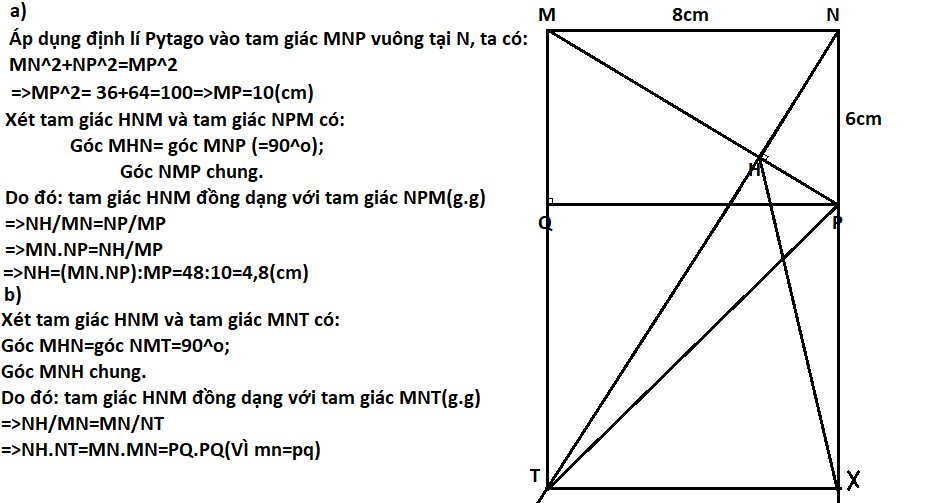
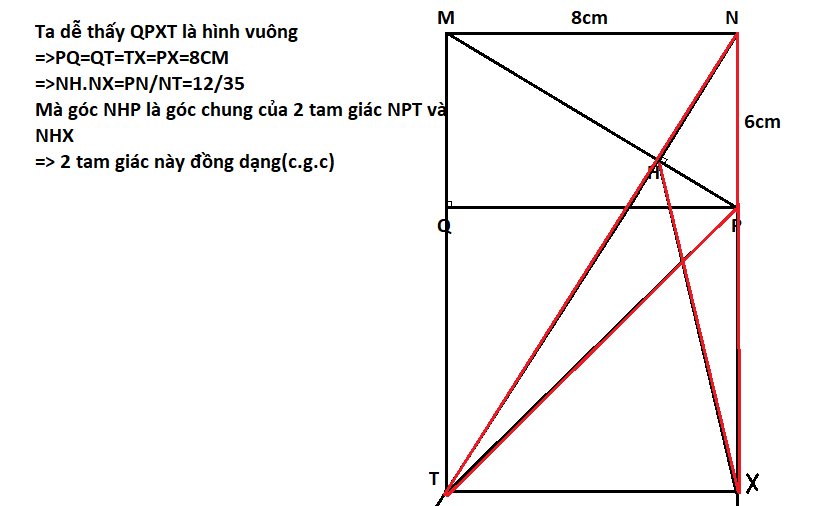
Cho hcn MNPQ có MQ=8,NP=6.Kẻ NH vuông góc MP tại H.
a;Tính MP,NH,HM,HP.
b;Gọi S à 1 điểm bất kì nằm giữa MH.Kẻ dg cao SA của tam giác SNP,SA cắt NH tại B.Kẻ dg cao thẳng vuông góc với SN tại S ,nó cắt PQ tại I.CM PB vuông góc SN
c;CM;SPBI là hình bình hành
d;Gỉa sử S là trung điểm MH .CM 2BN.PI=SH.MQ