cho f(x) là hàm đa thức thỏa mãn f(0) =-5 và f'(x) =f''(x) + 3x^2 -5 , với mọi x thuộc R . tìm nghiệm lớn nhất thuộc đoạn [-2020;2020] của phương trình f(sin^2 x) =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
11 tháng 10 2017
Chọn đáp án C
Phương pháp
Sử dụng công thức nguyên hàm:
![]()
dựa dữ kiện đề bài tìm được C, từ đó tính F(2)-F(-1)
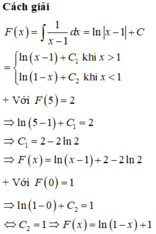


SS
10 tháng 5 2019
Đặt g(x)= p(x)- x^2 -2
Thay x =1 vào biểu thức trên ta có
g(1)= p(1)-3
Mà p(1)=3 => g(1)=0
thay x=3 vào biểu thức trên ta có
g(3)= p(3)- 3^2 -2
g(3)= 0
thay x=5 vào biểu thức trên ta có:
g(5)=0
=> x=1;x=3;x=5 là các nghiệm của g(x)
=> g(x)= (x-1)(x-3)(x-5)(x+a)
Mà p(x) = g(x)+x^2+2
=>p(x)= (x-1)(x-3)(x-5)(x+a)+ x^2 +2
=>p(-2)= (-2-1)(-2-3)(-2-5)(-2+a)+ (-2)^2 +2
=>p(-2)= 216-105a
7p(6)=896+105a
=> 7p(6)+ p(-2)= 1112
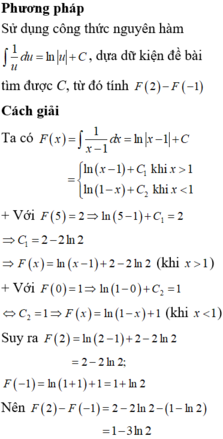

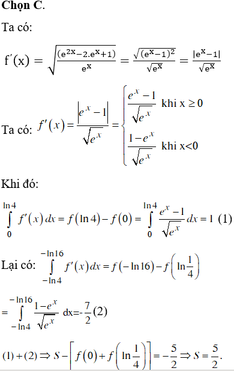
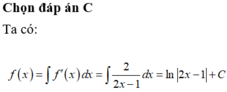
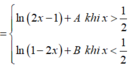
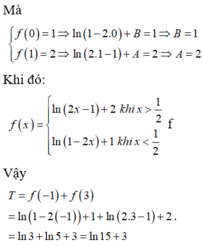
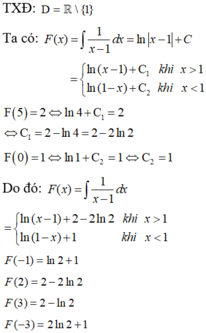
Giả sử \(f\left(x\right)\) có bậc k \(\Rightarrow f'\left(x\right)\) có bậc \(k-1\) và \(f''\left(x\right)\) có bậc \(k-2\)
\(\Rightarrow f''\left(x\right)+3x^2-5\) có bậc lớn nhất bằng \(max\left\{k-2;2\right\}\)
\(\Rightarrow k-1=max\left\{k-2;2\right\}\Rightarrow k-1=2\) (do \(k-1\ne k-2\) với mọi k)
\(\Rightarrow f\left(x\right)\) là đa thức bậc 3 có dạng: \(y=ax^3+bx^2+cx-5\) với \(a\ne0\)
\(3ax^2+2bx+c=6ax+2b+3x^2-5\)
\(\Leftrightarrow3ax^2+2bx+c=3x^2+6ax+2b-5\)
Đồng nhất 2 vế: \(\left\{{}\begin{matrix}3a=3\\2b=6a\\c=2b-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=3\\c=1\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=x^3+3x^2+x-5\)
Đặt \(sin^2x=t\Rightarrow0\le t\le1\)
\(f\left(t\right)=0\Leftrightarrow t^3+3t^2+t-5=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2+4t+5\right)=0\Rightarrow t=1\)
\(\Rightarrow sin^2x=1\Leftrightarrow cosx=0\)
\(\Rightarrow x=\frac{\pi}{2}+k\pi\)
\(\Rightarrow\frac{\pi}{2}+k\pi\le2020\Rightarrow k\le\frac{4040-\pi}{2\pi}\)
\(\Rightarrow k_{max}=642\Rightarrow x_{max}=\frac{\pi}{2}+642\pi\)