Cho hình bình hành ABCDcó tâm o chứng minh rằng AO-OB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2020
Câu 1: giả sử:\(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{OC}-\overrightarrow{OB}\Leftrightarrow\overrightarrow{BA}+\overrightarrow{AD}-\overrightarrow{BA}=\overrightarrow{OC}+\overrightarrow{BO}\)
\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\)(luôn đúng vì ABCD lad hình bình hành)
giả sử: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BC}-\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{BA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BB}+\overrightarrow{DD}=\overrightarrow{0}\)(LUÔN ĐÚNG)
câu 2 :GIẢ SỬ:
\(\overrightarrow{AB}+\overrightarrow{OA}=\overrightarrow{OB}\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{0}\)(luôn đúng)
giả sử: \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\\ \Leftrightarrow\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\)
NT
1
15 tháng 11 2023
\(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BO}+\overrightarrow{OC}=\overrightarrow{BC}\)(1)
ABCD là hình bình hành
=>\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}\)
=>\(\overrightarrow{BC}=\overrightarrow{BD}-\overrightarrow{BA}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BD}-\overrightarrow{BA}\)
CM
4 tháng 2 2019
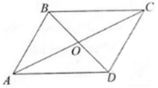
a) Ta có:
O là trung điểm của AC nên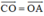 
Do đó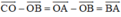 
b) ABCD là hình bình hành nên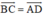 
Do đó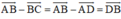 
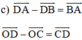
Mà ABCD là hình bình hành nên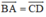 
Do đó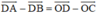 
d) ABCD là hình bình hành nên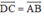 
Lại có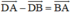 
Do đó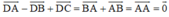 
15 tháng 11 2021
Vì △ABC vuông tại A (gt)
=> AB ⊥ AC
=> góc BAC = 90 độ
mà K ∈ AB; N ∈ AC
=> góc KAN = 90 độ
Xét tứ giác AKMN có :
góc MKA = 90 độ (MK ⊥ AB mà K ∈ AB)
góc KAN = 90 độ (cmt)
góc ANM = 90 độ (MN ⊥ ACmà N ∈ AC)
=> AKMN là hình chữ nhật (DHNB)
b) Vì AKMN là hình chữ nhật (cmt)
=> MN // AK mà K ∈ AB
=> MN // AB
Xét △ABC có : M là trung điểm BC (gt)
MN // AB (cmt)
=> N là trung điểm AC
=> NA = NC
mà NA = KM (vì AKMN là hình chữ nhật)
=> NC = KM
Xét tứ giác NKMC có : NC // KM ( KM // AN mà N ∈ AC)
NC = KM (cmt)
=> NKMC là hình bình hành (DHNB)
YP
21 tháng 10 2021
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành
NQ
0
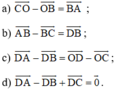
\(\overrightarrow{AO}-\overrightarrow{OB}=\overrightarrow{AO}-\overrightarrow{DO}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AD}\)