Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4 cm. Kẻ đường cao AK ( K thuộc Bc)
a) Chứng minh tam giác ABC đồng dạng với tam giác KBA
b) Tính độ dài đoạn thẳng BC, AK, BK, CK
c) Chứng minh: AB^2= BK.BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
15 tháng 5 2021
a/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
BK là pg \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AK}{CK}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=> \(\dfrac{AK}{3}=\dfrac{CK}{5}=\dfrac{AC}{8}=1\)
=> AK = 3cm ; CK = 5 cm
b/ Xét t/g ABC và t/g HBA có
\(\widehat{ABC}\) chung
\(\widehat{BAC}=\widehat{AHB}=90^o\)
=> t/g ABC ~ t/g HBA
=> \(\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
=> \(AB^2=BC.HB\)
c/ \(\dfrac{BC}{AC}=\dfrac{10}{6}=\dfrac{5}{3}\)
t/g ABC ~ t/g HBA vs tỉ số đồng dạng là 5/3
18 tháng 6 2019
a,Xét ∆ABC và ∆KBA có :
B là góc chung
BAC = BKA
=> ∆ ABC ĐỒNG DẠNG với ∆KBA
=>BA TRên KB = BC TRÊN BA
=>AB²= BK.BC
18 tháng 6 2019
https://h.vn/hoi-dap/question/585511.html
Bạn xem cả bài ở link này đi(mik gửi cho)
Học tôt!!!!!!!!!!!!
22 tháng 1
a: Ta có; ΔCAB vuông tại B
=>\(BA^2+BC^2=CA^2\)
=>\(CA^2=3^2+4^2=25\)
=>\(CA=\sqrt{25}=5\left(cm\right)\)
b: Xét ΔCBK vuông tại B và ΔCHK vuông tại H có
CK chung
\(\widehat{BCK}=\widehat{HCK}\)
Do đó: ΔCBK=ΔCHK
c: ta có: ΔCBK=ΔCHK
=>KB=KH
Xét ΔKBM vuông tại B và ΔKHA vuông tại H có
KB=KH
\(\widehat{BKM}=\widehat{HKA}\)(hai góc đối đỉnh)
Do đó: ΔKBM=ΔKHA
=>KM=KA
11 tháng 8 2021
a) Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
10 tháng 5 2022
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
Do đó: ΔABC\(\sim\)ΔHAC
b: Ta có: ΔABC\(\sim\)ΔHAC
nên AC/HC=BC/AC
hay \(AC^2=BC\cdot HC\)
c: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
10 tháng 5 2022
a, Xét Δ ABC và Δ HAC, có :
\(\widehat{ACB}=\widehat{HCA}\) (góc chung)
\(\widehat{BAC}=\widehat{AHC}=90^o\)
=> Δ ABC ∾ Δ HAC (g.g)
b, Ta có : Δ ABC ∾ Δ HAC (cmt)
=> \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
=> \(AC^2=BC.HC\)
c, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=3^2+4^2\)
=> \(BC^2=25\)
=> \(BC=5\left(cm\right)\)
16 tháng 6 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
9 tháng 5 2022
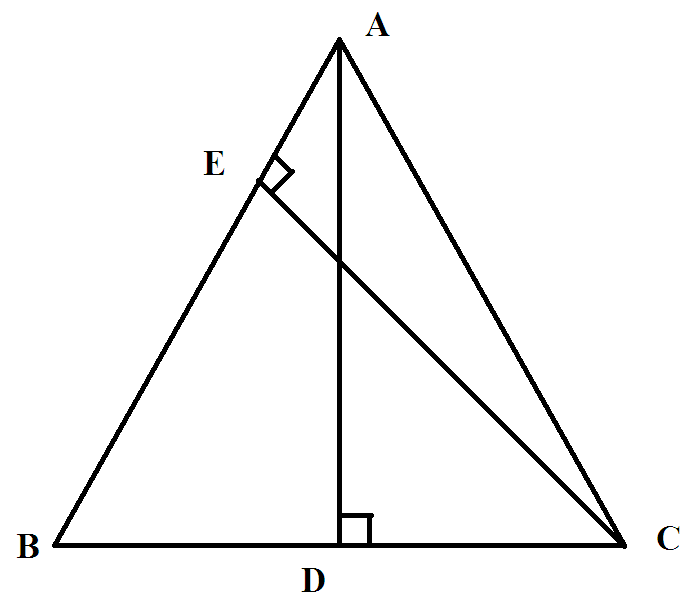
a) Xét △ABD và △CBE có:
\(\widehat{ADB}=\widehat{BEC}=90^o\)
\(\widehat{B}chung\)
Nên △ABD ∼ △CBE(g.g)
b)Theo câu a, ta có: △ABD ∼ △CB E
<=>\(\dfrac{AB}{BC}=\dfrac{BD}{BE}\Leftrightarrow AB.BE=BD.BC\)
c)Ta có:
\(BE=\dfrac{BD.BC}{AB}=\dfrac{3.12}{9}=4\left(cm\right)\)