Tìm tất cả các giá trị m để bất phương trình sau có nghiệm đúng với mọi x thuộc [-3;6]
\(\sqrt{3+x}+\sqrt{6-x}-\sqrt{\left(3+x\right)\left(6-x\right)}\le m\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bất phương trình đã cho 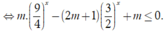
Đặt  Bất phương trình trở thành
Bất phương trình trở thành ![]()
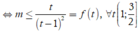
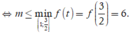
Chọn D.

\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(m-1\right)^2-\left(4m+8\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m^2-6m-7\le0\)
\(\Rightarrow-1\le m\le7\)
\(\Rightarrow m=\left\{-1;0;1;2;3;4;5;6;7\right\}\)

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 

Phương trình đã cho nghiệm đúng với ∀ x ∈ R hay phương trình có vô số nghiệm khi m 2 − 1 = 0 m − 1 = 0 ⇔ m = 1
Đáp án cần chọn là: A
Đặt \(\sqrt{3+x}+\sqrt{6-x}=t\Rightarrow3\le t\le3\sqrt{2}\)
\(t^2=9+2\sqrt{\left(3+x\right)\left(6-x\right)}\Rightarrow\sqrt{\left(3+x\right)\left(6-x\right)}=\frac{t^2-9}{2}\)
BPT trở thành:
\(t-\frac{t^2-9}{2}\le m\) ; \(\forall t\in\left[3;3\sqrt{2}\right]\)
\(\Leftrightarrow f\left(t\right)=-\frac{1}{2}t^2+t+\frac{9}{2}\le m\) ; \(\forall t\in\left[3;3\sqrt{2}\right]\)
\(\Leftrightarrow m\ge\max\limits_{\left[3;3\sqrt{2}\right]}f\left(t\right)\)
\(-\frac{b}{2a}=1\notin\left[3;3\sqrt{2}\right]\) ; \(f\left(3\right)=3\) ; \(f\left(3\sqrt{2}\right)=\frac{6\sqrt{2}-9}{2}< 3\)
\(\Rightarrow\max\limits_{\left[3;3\sqrt{2}\right]}f\left(t\right)=3\Rightarrow m\ge3\)