cho hai góc mOn và mOp kề bù biết 20% số đo góc mOn=3 phần 5 góc mOp tính số đo mỗi góc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)

Bài 2:
a: Ta có: Ox là tia phân giác của \(\widehat{mOn}\)
nên \(\widehat{mOx}=\widehat{nOx}=\dfrac{180^0}{2}=90^0\)
b: Ta có: Oy là tia phân giác của \(\widehat{mOx}\)
nên \(\widehat{yOx}=\dfrac{90^0}{2}=45^0\left(1\right)\)
Ta có: tia Ot là tia phân giác của \(\widehat{nOx}\)
nên \(\widehat{xOt}=\dfrac{90^0}{2}=45^0\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\widehat{xOy}=\widehat{xOt}\)

a)Có :\(\widehat{MOP}+\widehat{PON}=\widehat{MON}\)
\(\Rightarrow\widehat{MOP}+70^o=155^o\)
\(\Rightarrow\widehat{MOP}=85^o\)
b) Có :\(\widehat{QOM}+\widehat{MON}=180^o\)
\(\Rightarrow\widehat{QOM}+155^o=180^o\)
\(\Rightarrow\widehat{QOM}=25^o\)

vi moq=90
mop=90
nen moq=mop
to ko chac chan voi phan nay dau do con phan b to chua nhgi ra

CẬU SAO CHÉP ĐỀ BÀI XONG RÙI DÁN VÀO TÌM KẾM CÂU HỎI, CHỦ ĐỀ...
K CHO MK NHA

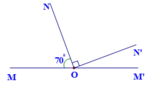
Vì M O N ^ , N O M ' ^ là hai góc kề bù nên:
M O N ^ + N O M ' ^ = 180 0 ⇒ 70 0 + N O M ' ^ = 180 0 ⇒ N O M ' ^ = 180 0 − 70 0 = 110 0
Ta có: O N ⊥ O N ' ⇒ N O N ' ^ = 90 0
Mà ON’trong góc NOM’ nên:
M ' O N ' ^ + N O N ' ^ = N O M ' ^ ⇒ M ' O N ' ^ + 90 0 = 110 0 ⇒ M ' O N ' ^ = 110 0 − 90 0 = 20 0