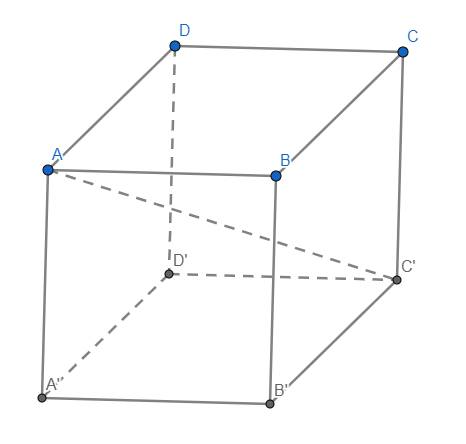
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm AB, BC và BB'. Khi đó thiết diện do mặt phẳng (MNP) cắt hình lập phương là hình gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 12 2023
Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
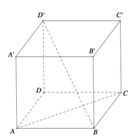
\(\overrightarrow{BD}.\overrightarrow{D'C}=\overrightarrow{BD}\left(\overrightarrow{D'D}+\overrightarrow{DC}\right)=\overrightarrow{BD}.\overrightarrow{D'D}+\overrightarrow{BD}.\overrightarrow{DC}\)
\(=\overrightarrow{BD}.\overrightarrow{DC}=-\overrightarrow{DB}.\overrightarrow{DC}=-a\sqrt{2}.a.cos45^0=-a^2\)
CM
29 tháng 1 2017
Đáp án C
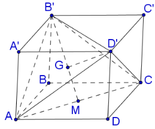
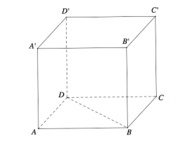
Nhận thấy chóp ACD′B′ có tất cả các
cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là
trọng tâm của tam giác AB′C′.
Chóp ACD′B′ nhận D′G là đường cao.
Xét tam giác AB′C′ có
1N
0
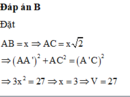
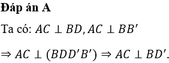
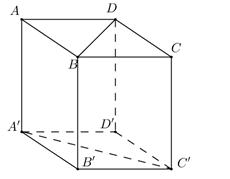
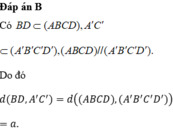
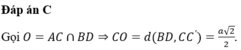
Nối MN cắt CB kéo dài tại E
Nối EP kéo dài cắt B'C' tại F
Nối NP cắt A'B' kéo dài tại G
Nối GF kéo dài cắt C'D' tại H và A'D' kéo dài tại K
Nối MK cắt DD' tại Q
Thiết diện là lục giác MNPFHQ (lục giác này 6 cạnh dài bằng nhau và bằng 1 nửa đường chéo các mặt bên)