chứng minh 3 đường phân giác trong tam giác đều vừa là đường trung trực vừa là đường phân giác của tam giác đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

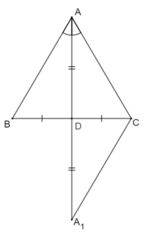
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)

⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 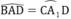 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
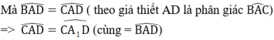
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

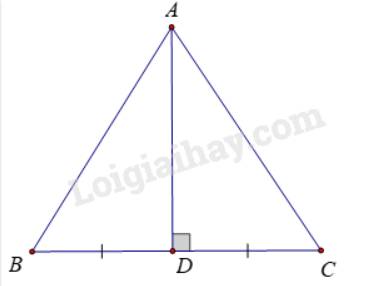
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
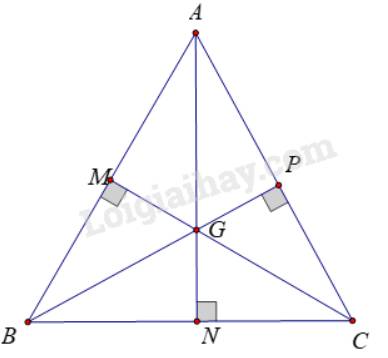
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất

- MÔN ĐẠI CƯƠNG
- ÔN THI ĐẠI HỌC
- TOÁN HỌC
- NGỮ VĂN
- ANH VĂN
- VẬT LÝ
- HÓA HỌC
- SINH HỌC
- LỊCH SỬ
- ĐỊA LÝ
- TRUYỆN CỔ TÍCH
- Sóng - Xuân Quỳnh
- Đàn ghi ta của Lor-ca - Thanh Thảo
Bài 42 trang 73 sgk toán lớp 7- tập 2
Cập nhật lúc: 08/07/2014 17:21 pm Danh mục: Toán lớp 7
Chứng minh định lí- Bài 38 trang 73 sgk toán lớp 7- tập 2
- Bài 40 trang 73 sgk toán lớp 7- tập 2
- Bài 36 trang 72 sgk toán lớp 7- tập 2
- Bài 42 trang 73 sgk toán lớp 7- tập 2
- Bài 39 trang 73 sgk toán lớp 7- tập 2
Xem thêm: Tính chất ba đường phân giác của tam giác
42. Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
Gợi ý : Trong ∆ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn AD1 sao cho DA1 = AD
Hướng dẫn:
Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD

Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân

Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.

cho em giải khác nhé
D thuộc phân giác góc A suy ra DH = DG ( tính chất tia phân giác của một góc )
xét hai tam giác vuông BHD và CGD có
DH = DG ( cmt)
DB = DC ( gt)
do đó tam giác BHD = tam giác CGD ( cạnh huyền - góc nhọn )
suy ra góc B = góc C ( 2 góc tương ứng )
tam giác ABC có góc B = góc C suy ra tam giác ABC cân tại A
Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD

Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân

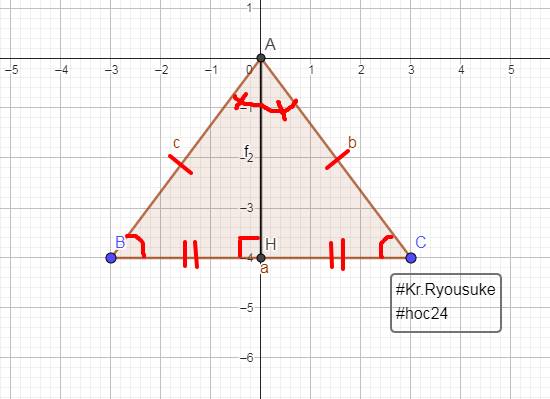
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao của} \Delta ABC)$
`=> \Delta ABH = \Delta ACH (ch-gn)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 cạnh tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`
`c,`
Vì `\Delta ABH = \Delta ACH (a)`
`-> \text {HB = HC}`
Ta có:
`\text {AH} \bot \text {BC}`
`\text {HB = HC}`
`-> \text {AH là đường trung trực của}` `\Delta ABC`.

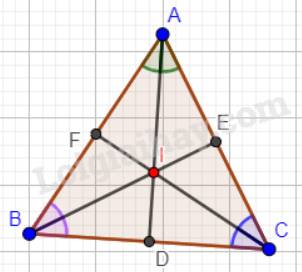
Ta có: I là giao điểm của ba đường phân giác của tam giác ABC. Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: \(ID \bot BC;IE \bot AC;IF \bot AB\).
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\)(vì \(ID \bot BC\)).
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta BEA = \Delta BEC\)(g.c.g). Suy ra: BA = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.