Cho A(2,1), B(3,-2). tập hợp những điểm M(x;y) sao cho \(MA^2+MB^2=30\) là một đường tròn có pt bán kính bằng??
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: 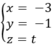

a. Tập hợp con của tập hợp M gồm những số có 1 chữ số là : 1 ; 2 ; 3 ; 4 ;.....; 8 ; 9
b . Tập hợp con của tập hợp hợp M gồm những số chẵn có chẵn có 3 chữ số là : 100 ; 102 ; 104 ; ,.......... ; 996 ; 998

Chọn B.
Theo giả thiết
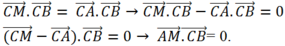
Tập hợp điểm M là đường thẳng đi qua A và vuông góc với BC.

Chọn A.
Theo giải thiết
![]()
![]()
Tập hợp điểm M là đường tròn đường kính BC.
\(\left\{{}\begin{matrix}\overrightarrow{AM}=\left(x-2;y-1\right)\\\overrightarrow{BM}=\left(x-3;y+2\right)\end{matrix}\right.\)
\(MA^2+MB^2=30\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-1\right)^2+\left(x-3\right)^2+\left(y+2\right)^2=30\)
\(\Leftrightarrow2x^2-10x+2y^2+2y-12=0\)
\(\Leftrightarrow x^2-5x+y^2+y-6=0\)
\(\Leftrightarrow\left(x-\frac{5}{2}\right)^2+\left(y+\frac{1}{2}\right)^2=\frac{25}{2}\)
Đường tròn có bán kính \(R=\sqrt{\frac{25}{2}}=\frac{5\sqrt{2}}{2}\)