bai nay lam ntn the moi nguoi :(
Cho hình chóp SABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = a căn2 gọi H,K lần lượt là hình chiếu của A lên SB và SD tìm góc giữa 2 mp (AHK) và (ABCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow\Delta SAB\) vuông cân \(\Rightarrow\left\{{}\begin{matrix}SA=AB=a\\SB=a\sqrt{2}\end{matrix}\right.\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
\(\dfrac{V_{SAHIK}}{V_{SABCD}}=\dfrac{2V_{SAHI}}{2V_{SABC}}=\dfrac{V_{SAHI}}{V_{SABC}}=\dfrac{SH}{SB}.\dfrac{SI}{SC}=\left(\dfrac{SA}{SB}\right)^2\left(\dfrac{SA}{SC}\right)^2=\left(\dfrac{a}{a\sqrt{2}}\right)^2\left(\dfrac{a}{a\sqrt{3}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SAIHK}=\dfrac{1}{6}V_{SABCD}=\dfrac{1}{6}.\dfrac{1}{3}.SA.AB^2=\dfrac{a^3}{18}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
Bạn coi lại đề, AHIK là 1 tứ giác nên ko thể có thể tích
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
\(\dfrac{V_{SAHKE}}{V_{SABCD}}=\dfrac{2V_{SAHK}}{2V_{SABC}}=\dfrac{V_{SAHK}}{V_{SABC}}\)
\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.BC=\dfrac{a^3}{3}\); \(V_{SABCD}=\dfrac{2a^3}{3}\)
\(\dfrac{SH}{SB}=\dfrac{SA^2}{SB}:SB=\left(\dfrac{SA}{SB}\right)^2\); \(\dfrac{SK}{SC}=\dfrac{SA^2}{SC}:SC=\left(\dfrac{SA}{SC}\right)^2\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{6}\)
\(\dfrac{V_{SAHK}}{V_{SABC}}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAHKE}=\left(\dfrac{2a}{a\sqrt{5}}\right)^2.\left(\dfrac{2a}{a\sqrt{6}}\right)^2.\dfrac{2a^3}{3}=\dfrac{16a^3}{45}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2023
Kẻ AE vuông góc SC (E thuộc SC)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\)
\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\Rightarrow SC\perp\left(AMN\right)\)
Mà \(AE\perp SC\Rightarrow E\in\left(AMN\right)\)
\(\Rightarrow AE\) là hình chiếu vuông góc của SA lên (AMN)
\(\Rightarrow\widehat{SAE}\) là góc giữa SA và (AMN)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{SA^2+AC^2}=2a\)
\(\Delta SAC\) vuông cân tại A \(\Rightarrow AE=SE=\dfrac{1}{2}SC=a\)
\(\Rightarrow\Delta SAE\) vuông cân tại E \(\Rightarrow\widehat{SAE}=45^0\)
TN
21 tháng 1 2021
a) Xét tam giác SAB và tam giác SAD có:
+) Chung SA
+) \(AB=AD\)
+) \(\widehat{SAB}=\widehat{SAD}=90^0\) (Vì \(SA\perp\left(ABCD\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AD\end{matrix}\right.\) )
\(\Rightarrow\Delta SAB=\Delta SAD\left(c-g-c\right)\)
\(\Rightarrow\widehat{SAB}=\widehat{SAD}\)
\(\Rightarrow\Delta SAH=\Delta SAK\left(ch-gn\right)\)
\(\Rightarrow SH=SK\)
Mà SB=SD (Do \(\Delta SAB=\Delta SAD\))
\(\Rightarrow\dfrac{SH}{SB}=\dfrac{SK}{SD}\)
\(\Rightarrow\)HK||BD( Áp dụng Talet cho tam giác SBD)
b)Đặt SA=x, AB=y
Gọi O là tâm của đáy (ABCD), trong mp(SAC) cho SO cắt AI tại J
Ta tính được \(SC=\sqrt{x^2+2y^2}\) và SO=\(\sqrt{x^2+\dfrac{y^2}{2}}\)
Áp dụng định lí cos cho tam giác OSC có:
\(2SO.SC.\cos OSC=SO^2+SC^2-OC^2=x^2+\dfrac{y^2}{2}+x^2+2y^2-\dfrac{y^2}{2}=2x^2+2y^2\)
\(\Rightarrow SO.SC.cosOSC=x^2+y^2\)
\(\dfrac{SJ}{SO}=\dfrac{SI}{SO.cosOSC}=\dfrac{SA^2}{SC.SO.cosOSC}=\dfrac{x^2}{x^2+y^2}\left(1\right)\)
\(SK=\dfrac{SA^2}{SD}\Rightarrow\dfrac{SK}{SD}=\dfrac{SA^2}{SD^2}=\dfrac{x^2}{x^2+y^2}\left(2\right)\)
Từ (1) và (2), áp dụng định lí Talet đảo cho tam giác SDO ta có KJ||DO hay KJ||BD
Chứng minh tương tự ta có: JH||BD
Mà HK||BD nên K,H,J thẳng hàng
\(\Rightarrow\exists1\) mặt phẳng chứa 4 điểm A,H,I,K (Vì AI cắt HK tại J)
\(\Rightarrow I\in mp\left(AHK\right)\)(đpcm)
Ta có: \(\left\{{}\begin{matrix}BD\perp AC\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\Rightarrow BD\perp\left(SAC\right)\)
Mà HK||BD
\(\Rightarrow HK\perp\left(SAC\right)\left(đpcm\right)\)
CM
5 tháng 11 2018
Chọn đáp án A
+ Ta có
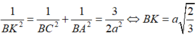
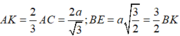
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
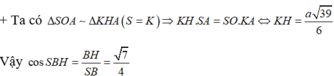
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)
Kẻ \(AP\perp SC\)
Dễ dàng chứng minh \(SC\perp\left(AHK\right)\) \(\Rightarrow AP\in\left(AHK\right)\)
\(\Delta SAB=\Delta SAD\Rightarrow\left\{{}\begin{matrix}SH=SK\\SB=SD\end{matrix}\right.\) \(\Rightarrow\frac{SH}{SB}=\frac{SK}{SD}\Rightarrow HK//BD\)
Mà \(BD\perp\left(SAC\right)\Rightarrow HK\perp\left(SAC\right)\)
Lại có \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow\) \(\widehat{CAP}\) là góc giữa (AHK) và (ABCD)
\(AC=a\sqrt{2}\) ; \(\frac{1}{AP^2}=\frac{1}{AC^2}+\frac{1}{SA^2}\Rightarrow AP=\frac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{CAP}=\frac{AP}{AC}=\frac{\sqrt{2}}{2}\Rightarrow\widehat{CAP}=45^0\)
(Hoặc tam giác SAC vuông cân tại A nên AP là đường cao đồng thời là phân giác \(\Rightarrow\widehat{CAP}=\frac{1}{2}\widehat{SAC}=\frac{1}{2}.90^0=45^0\) )