x2-2x+m+2=0 với x12+x22+4x1x2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
1
10 tháng 4 2023
Δ=(-2)^2-4(-2m+1)
=4+8m-4=8m
Để phương trình có nghiệm thì 8m>=0
=>m>=0
\(x_2^2\left(x_1^2-1\right)+x_1^2\left(x_2^2-1\right)=8\)
=>\(2\cdot\left(x_1\cdot x_2\right)^2-x_2^2-x_1^2=8\)
=>\(2\cdot\left(-2m+1\right)^2-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=8\)
=>\(2\left(2m-1\right)^2-\left[2^2-2\left(-2m+1\right)\right]=8\)
=>\(8m^2-8m+2-4+2\left(-2m+1\right)=8\)
=>\(8m^2-8m-2-4m+2-8=0\)
=>8m^2-12m-8=0
=>m=2 hoặc m=-1/2(loại)
27 tháng 3 2021
Sửa đề: \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\)
Ta có: \(\Delta=2^2-4\cdot1\cdot\left(m-3\right)=4-4m+12=-4m+16\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow-4m+16>0\)
\(\Leftrightarrow-4m>-16\)
hay m<4
Khi m<4, Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1\cdot x_2=m-3\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2\cdot x_1\cdot x_2+2\left(x_1\cdot x_2\right)^2=7\cdot x_1\cdot x_2\)
\(\Leftrightarrow\left(-2\right)^2-2\cdot\left(m-3\right)+2\cdot\left(m-3\right)^2=7\left(m-3\right)\)
\(\Leftrightarrow4-2m+6+2\left(m^2-6m+9\right)=7m-21\)
\(\Leftrightarrow-2m+10+2m^2-12m+18-7m+21=0\)
\(\Leftrightarrow2m^2-21m+49=0\)
\(\Leftrightarrow2m^2-14m-7m+49=0\)
\(\Leftrightarrow2m\left(m-7\right)-7\left(m-7\right)=0\)
\(\Leftrightarrow\left(m-7\right)\left(2m-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-7=0\\2m-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=7\left(loại\right)\\2m=7\end{matrix}\right.\Leftrightarrow m=\dfrac{7}{2}\left(nhận\right)\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\) thì \(m=\dfrac{7}{2}\)
27 tháng 3 2021
Ta có: x2 + 2x + m - 3 = 0
Theo hệ thực Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=m-3\end{matrix}\right.\) (I)
Ta có: x12 + x22 + 2(x1x2)2 = 7x1x2
\(\Leftrightarrow\) (x1 + x2)2 - 2x1x2 + 2(x1x2)2 = 7x1x2 (*)
Thay (I) vào (*) ta được:
(-2)2 - 2(m - 3) + 2(m - 3)2 = 7(m - 3)
\(\Leftrightarrow\) 4 - 9m + 27 + 2(m2 - 6m + 9) = 0
\(\Leftrightarrow\) 31 - 9m + 2m2 - 12m + 18 = 0
\(\Leftrightarrow\) 2m2 - 21m + 49 = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}m=7\\m=3,5\end{matrix}\right.\)
Vậy ...
Chúc bn học tốt!
CM
5 tháng 5 2018
Khi đó phương trình trở thành:
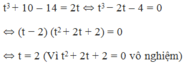
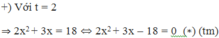
Giả sử x 1 , x 2 là hai nghiệm của phương trình (*)
Theo Vi – et, ta có x 1 + x 2 = − 3 2 x 1 . x 2 = − 9
⇒ A = x 1 2 + x 2 2 − 4 x 1 x 2 = x 1 + x 2 2 − 6 x 1 . x 2 = 9 4 + 54 = 225 4 = 15 2
Đáp án cần chọn là: D
7 tháng 1 2023
Δ=(-2)^2-4(m-3)
=4-4m+12=-4m+16
Để pt có hai nghiệm thì -4m+16>=0
=>-4m>=-16
=>m<=4
x1^2+x2^2-x1x2<7
=>(x1+x2)^2-3x1x2<7
=>2^2-3(m-3)<7
=>4-3m+9<7
=>-3m+13<7
=>-3m<-6
=>m>2
=>2<m<=4
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2023
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=3m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(3m-1\right)=10\)
\(\Leftrightarrow m=-\dfrac{2}{3}\)
GH
5 tháng 7 2023
Bổ sung thêm điều kiện đề với \(m\ne1\) nữa nhé: )
Nhẩm nghiệm: \(a-b+c=0\) \(\left(m-1-m-1+2=0\right)\)
\(\Rightarrow\) PT có 2 nghiệm \(x_1=-1;x_2=\dfrac{2}{m-1}\)
Nếu \(x_1^2-x_2^2=3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=3\)
=> Không có giá trị m thỏa mãn.
Nếu \(x_1^2-x_2^2=-3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=-3\\ \Rightarrow m=2\left(TM\right)\)
CM
12 tháng 6 2018
c) Theo định lí Vi-et ta có:
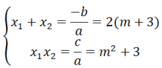
P = x 1 2 + x 2 2 = (x1 + x2 )2 - 2 x 1 x 2 = 4 m + 3 2 - 2( m 2 + 3)
= 4( m 2 + 6m + 9) - 2( m 2 + 3) = 2 m 2 + 24m + 30
Ta có \(\Delta'=\left(-1\right)^2-\left(m+2\right)\)
\(=-m-1\ge0\)\(\Leftrightarrow m\le-1\)
Áp dụng hệ thức Vi-ét ta có :
\(\hept{\begin{cases}x_1+x_2=2\left(1\right)\\x_1x_2=m+2\left(2\right)\end{cases}}\)
Ta có : \(x_1^2+x_2^2+4x_1x_2=0\)
\(x_1^2+2x_1x_2+x_2^2+2x_1x_2=0\)
\(\left(x_1+x_2\right)^2+2x_1x_2=0\)
Thay (1),(2) vào biểu thức ta có:
\(2^2+2\left(m+2\right)=0\)
\(4+2m+4=0\)
\(2m=-8\)
\(m=-4\left(TM\right)\)
VẬY KHI m=-4 THÌ PHƯƠNG TRÌNH TM ĐỀ BÀI