Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình có 2 nghiệm phân biệt khi:
\(\Delta'=1-\left(m-1\right)>0\Rightarrow m< 2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(m-1\right)=10\)
\(\Leftrightarrow m=-2\) (thỏa mãn)

bạn tìm đenta
sau đó cho đenta >0
theo hệ thức viets tính đc x1+x2, x1*x2
bình phương 2 vế của pt thỏa mãn thế x1, x2 tương ứng là tìm dc m
mik chỉ nêu ý chình thôi nha mik hơi bận

có 2 nghiệm phân biệt chi và chỉ khi \(\Delta^,=\left(m-2\right)^2-m^2-2m+3>0\)
\(\Leftrightarrow m^2-4m+4-m^2-2m+3>0\)
\(\Leftrightarrow-6m+7>0\Leftrightarrow m< \frac{7}{6}\)

a/
PT có nghiệm \(x=\sqrt{2}\Rightarrow\left(m-1\right).2-2m.\sqrt{2}+m-2=0\)
\(\Leftrightarrow\left(3-2\sqrt{2}\right)m=4\Leftrightarrow m=\frac{4}{3-2\sqrt{2}}\)
b/
\(\left(m-1\right)x^2-2mx+m-2=0\text{ (1)}\)
\(+m-1=0\Leftrightarrow m=1\text{ thì }\left(1\right)\text{ trở thành }-2x+1-2=0\Leftrightarrow x=-\frac{1}{2}\)(loại do chỉ có 1 nghiệm)
\(+m-1\ne0\Leftrightarrow m\ne1\)
\(\left(1\right)\text{ là một phương trình bậc 2 ẩn }x.\)
\(\left(1\right)\text{ có 2 nghiệm phân biệt }\Leftrightarrow\Delta'=m^2-\left(m-1\right)\left(m-2\right)>0\)
\(\Leftrightarrow3m-2>0\Leftrightarrow m>\frac{2}{3}\)

a) pt (1) có 2 nghiệm dương phân biệt => \(\hept{\begin{cases}\Delta_1=1-4m>0\\m>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< \frac{1}{4}\\m>0\end{cases}}\Leftrightarrow0< m< \frac{1}{4}\)
pt (2) có 2 nghiệm dương phân biệt => \(\hept{\begin{cases}\Delta_2=1-4m>0\\\frac{1}{m}>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< \frac{1}{4}\\m>0\end{cases}}\Leftrightarrow0< m< \frac{1}{4}\)
=> để 2 pt có 2 nghiệm dương phân biệt thì \(0< m< \frac{1}{4}\)
b) \(x_1x_2x_3+x_2x_3x_4+x_3x_4x_1+x_4x_1x_2=x_1x_2\left(x_3+x_4\right)+x_3x_4\left(x_1+x_2\right)=m.\frac{1}{m}+\frac{1}{m}.1=\frac{1}{m}+1>\frac{1}{\frac{1}{4}}+1=5\)
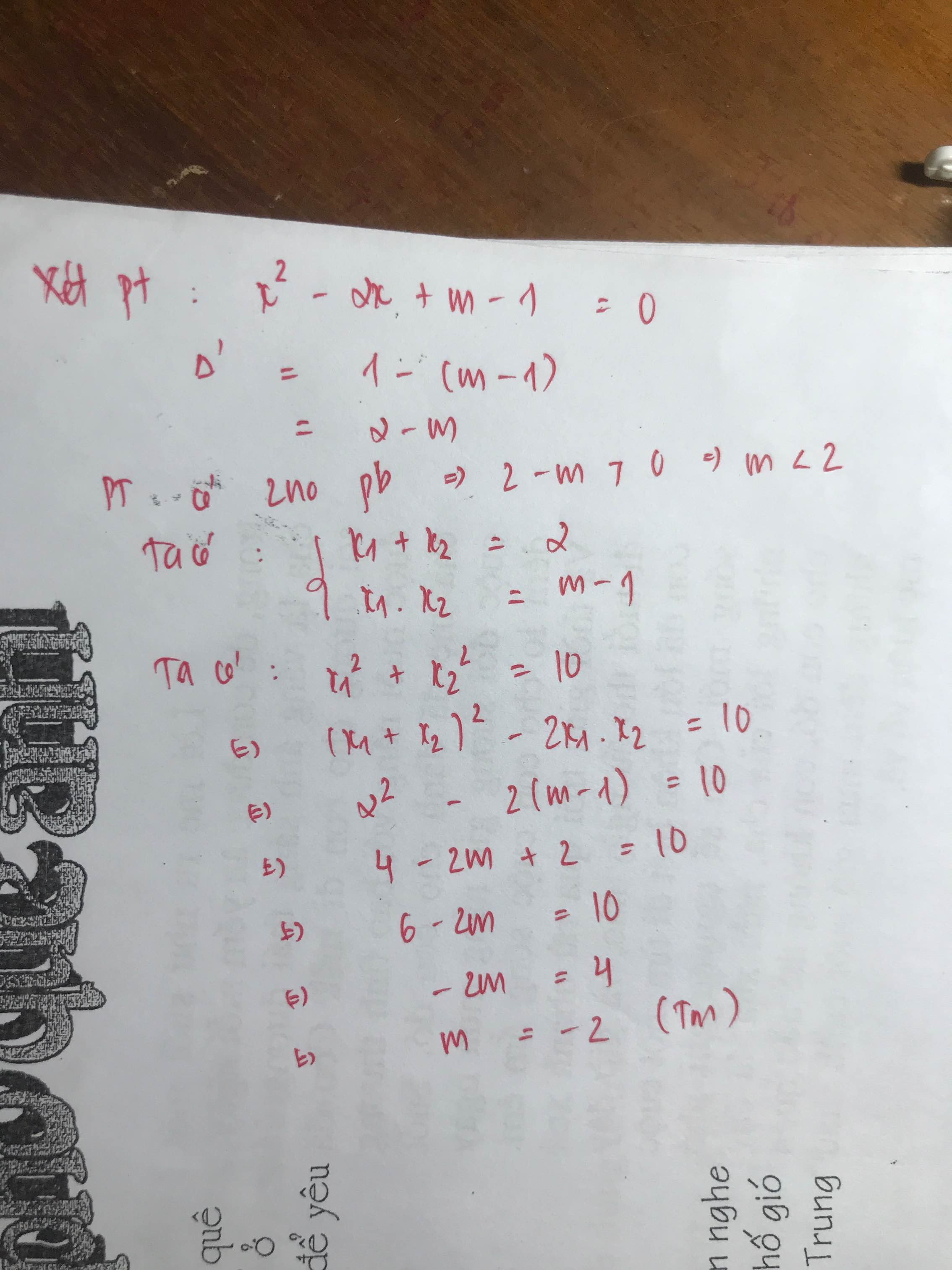
Sửa đề: \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\)
Ta có: \(\Delta=2^2-4\cdot1\cdot\left(m-3\right)=4-4m+12=-4m+16\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow-4m+16>0\)
\(\Leftrightarrow-4m>-16\)
hay m<4
Khi m<4, Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1\cdot x_2=m-3\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2\cdot x_1\cdot x_2+2\left(x_1\cdot x_2\right)^2=7\cdot x_1\cdot x_2\)
\(\Leftrightarrow\left(-2\right)^2-2\cdot\left(m-3\right)+2\cdot\left(m-3\right)^2=7\left(m-3\right)\)
\(\Leftrightarrow4-2m+6+2\left(m^2-6m+9\right)=7m-21\)
\(\Leftrightarrow-2m+10+2m^2-12m+18-7m+21=0\)
\(\Leftrightarrow2m^2-21m+49=0\)
\(\Leftrightarrow2m^2-14m-7m+49=0\)
\(\Leftrightarrow2m\left(m-7\right)-7\left(m-7\right)=0\)
\(\Leftrightarrow\left(m-7\right)\left(2m-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-7=0\\2m-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=7\left(loại\right)\\2m=7\end{matrix}\right.\Leftrightarrow m=\dfrac{7}{2}\left(nhận\right)\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\) thì \(m=\dfrac{7}{2}\)
Ta có: x2 + 2x + m - 3 = 0
Theo hệ thực Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=m-3\end{matrix}\right.\) (I)
Ta có: x12 + x22 + 2(x1x2)2 = 7x1x2
\(\Leftrightarrow\) (x1 + x2)2 - 2x1x2 + 2(x1x2)2 = 7x1x2 (*)
Thay (I) vào (*) ta được:
(-2)2 - 2(m - 3) + 2(m - 3)2 = 7(m - 3)
\(\Leftrightarrow\) 4 - 9m + 27 + 2(m2 - 6m + 9) = 0
\(\Leftrightarrow\) 31 - 9m + 2m2 - 12m + 18 = 0
\(\Leftrightarrow\) 2m2 - 21m + 49 = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}m=7\\m=3,5\end{matrix}\right.\)
Vậy ...
Chúc bn học tốt!