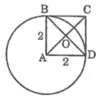
Cho điểm A nằm ngoài đường tròn (O;R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) ( B, C là các tiếp điểm). Vẽ đường kính BD của (O), gọi H là giao điểm của OA và BC.
a) Cmr : BC vuông góc với OA, BC vuông góc với CD.
b) Gọi E là giao điểm của AD và đường tròn (O) ( E \(\ne\) D).
Chứng minh: OH.OA=R2 và DE.DA=4.OH.OA
c) Gọi M là giao điểm của BC và AD, N là giao điểm của OA và BE.
Chứng minh : MN song song BD
d) Tiếp tuyến tại D của đường tròn (O) cắt BC tại F. Gọi K là giao điểm của AD và OF.
Giả sử AB= \(R\sqrt{5}\). Tính độ dài đoạn thẳng KE theo R.