25x2-480x+400=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 9 2023
\(25x^2-9=0\\ \Leftrightarrow\left(5x-3\right)\left(5x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x=3\\5x=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\\x=\dfrac{3}{5}\end{matrix}\right.\)
7 tháng 9 2023
=>(5x-3)(5x+3)=0
=>5x-3=0 hoặc 5x+3=0
=>x=3/5 hoặc x=-3/5
PT
1
CM
28 tháng 1 2018
Ta có: - 2 5 x 2 - 7 3 x = 0 ⇔ 6 x 2 + 35x = 0 ⇔ x(6x + 35) = 0
⇔ x = 0 hoặc 6x + 35 = 0 ⇔ x = 0 hoặc x = -35/6 .
Vậy phương trình có hai nghiệm x 1 = 0, x 2 = -35/6
2 tháng 10 2021
\(-25x^2+5x-1=-\left(25x^2-5x+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(5x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}< 0\forall x\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 7 2023
Ta có:
\(P=\dfrac{5x-4y}{5x+4y}\)
\(\Leftrightarrow P^2=\left(\dfrac{5x-4y}{5x+4y}\right)^2\)
\(\Leftrightarrow P^2=\dfrac{\left(5x-4y\right)^2}{\left(5x+4y\right)^2}\)
\(\Leftrightarrow P^2=\dfrac{\left(5x\right)^2-2\cdot5x\cdot4y+\left(4y\right)^2}{\left(5x\right)^2+2\cdot5x\cdot4y+\left(4y\right)^2}\)
\(\Leftrightarrow P^2=\dfrac{\left(25x^2+16y^2\right)-40xy}{\left(25x^2+16y^2\right)+40xy}\)
Thay \(25x^2+16y^2=50xy\) vào ta có:
\(P^2=\dfrac{50xy-40xy}{50xy+40xy}=\dfrac{10xy}{90xy}=\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\)
Mà: \(4y< 5x< 0\)
Nên: \(P=\dfrac{5x-4y}{5x+4y}< 0\)
Vậy: \(P=-\dfrac{1}{3}\)
27 tháng 7 2023
25x^2+16y^2=50xy
=>25x^2-50xy+16y^2=0
=>25x^2-10xy-40xy+16y^2=0
=>5x(5x-2y)-8y(5x-2y)=0
=>(5x-2y)(5x-8y)=0
=>5x=2y hoặc 5x=8y
5x>4y
=>5x=8y
=>x/8=y/5=k
=>x=8k; y=5k
\(P=\dfrac{5\cdot8k-4\cdot5k}{5\cdot8k+4\cdot5k}=\dfrac{40-20}{40+20}=\dfrac{1}{3}\)
NT
1
CM
10 tháng 1 2018
Biểu thức x 2 - 25 x 2 - 10 x + 25 x xác định khi x 0 và x ≠ 5.
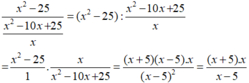
Ta có: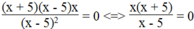 
khi x(x + 5) = 0 và x – 5
≠
0
x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5
x = 0 không thỏa mãn điều kiện.
Vậy x = - 5 thì biểu thức x 2 - 25 x 2 - 10 x + 25 x có giá trị bằng 0.
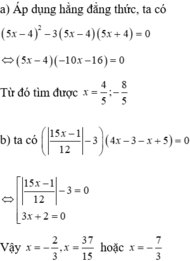
25x2-480x+400=0
\(\Leftrightarrow\left[{}\begin{matrix}25x^2=0\\-480x+400=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-25\\-480x=-400\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-25\\x=\frac{5}{6}\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(x=\frac{5}{6}\)