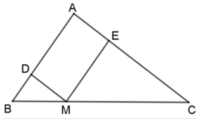
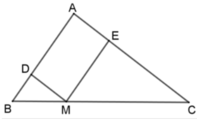
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MB/MC=1/2.
Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 24cm, tính chu vi của các tam giác DBM và EMC.
PHẢI VẼ HÌNH