Cho a,b,c là các số nguyên lẻ. Chứng minh P(x) = ax2+bx+c không có nghiệm nguyên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 1 2016
BÀI TOÁN PHỤ: CHứng minh rằng số chính phương lẻ chia cho 8 dư 1.
Giải: Xét số chính phương lẻ là \(m^2\left(m\in Z\right)\)
Như vậy m là số lẻ, đặt \(m=2n+1\)
Ta có:
\(m^2=\left(2n+1\right)^2=4n^2+4n+1=4.n.\left(n+1\right)+1\)
Vì n(n+1) là tích 2 số nguyên liên tiếp nên chia hết cho 2
\(\Rightarrow4n\left(n+1\right) \) chia hết cho 8
\(\Rightarrow4.n.\left(n+1\right)+1\) chia 8 dư 1
Vậy ta có điều phải chứng minh.
Vì a lẻ nên \(a\ne0\), phương trình \(ax^2+bx+c=0\) là phương trình bậc hai.
Xét \(\Delta=b^2-4ac\): b lẻ, theo bài toán phụ có \(b^2=8k+1\left(k\in Z\right)\)
a,c lẻ \(\Rightarrow\) \(ac\) lẻ
Đặt \(ac=2l-1\left(l\in Z\right)\)
Do đó \(\Delta=b^2-4ac=8k+1-4.\left(2l-1\right)=8k+1-8l+4=8\left(k-l\right)+5 \)chia cho 8 dư 5, theo bài toán phụ trên ta có \(\Delta\) không phải số chính phương.
\(\Delta\) là số nguyên, không phải óố chính phương \(\Rightarrow\sqrt{\Delta}\) là số vô tỉ
Nghiệm của phương trình đã cho (nếu có) là: \(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)
b,a\(\in Z\), \(\sqrt{\Delta}\) vô tỉ nên x là vô tỉ.
Vậy phương trình có nghiệm nếu có thì các nghiệm ấy không thể là số hữu tỉ.
ơng là phươngax2+bx+c=0
10 tháng 11 2016
Giả sử f(0), f(1), f(2) có giá trị nguyên là m,n,p. Theo đề bài ta có
\(1\hept{\begin{cases}c=m\left(1\right)\\a+b+c=n\left(2\right)\\4a+2b+c=p\left(3\right)\end{cases}}\)
Ta lấy (3) - 2(2) + (1) vế theo vế ta được
2a = p - 2n + m
=> 2a là số nguyên
Ta lấy 4(2) - (3) - 3(1) vế theo vế ta được
2b = 4n - p - 3m
=> 2b cũng là số nguyên
12 tháng 4 2017
*f(0) nguyên suy ra 0+0+c=c nguyên
*Vì c nguyên và f(1)=a+b+c nguyên suy ra a+b nguyên
*Tương tự vs f(2)=4a+2b+c suy ra 2a nguyên (Vì 4a+2b và 2(a+b) đều nguyên)
Vì 2a và 2(a+b) nguyên suy ra 2b nguyên (đpcm)
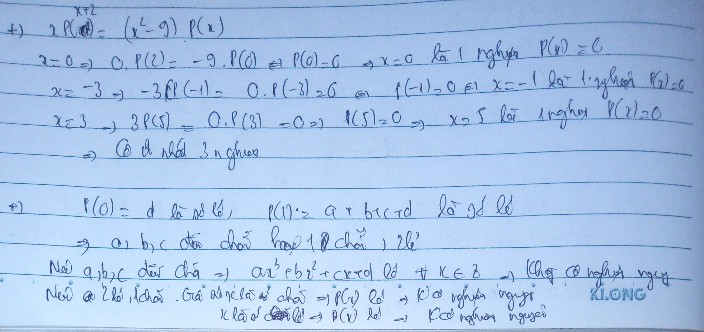
tju6i