Cho ba điểm A(1-2m; 4m), B(2m;1-m), C(3m-1;0). Gọi G là trọng tâm ABC thì G nằm trên đường thẳng nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)

Đáp án B.
Phương pháp: Tìm điều kiện để phương trình hoành độ giao điểm có ba nghiệm phân biệt thỏa mãn x A = 2 , hoặc x B < - 1 < x C < 1 hoặc - 1 < x B < 1 < x C
Cách giải:
Đồ thị hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 luôn đi qua điểm A(2;0)
Xét phương trình hoành độ giao điểm
x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 = 0
![]()
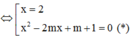
Để phương trình có 3 nghiệm phân biệt ó pt (*) có 2 nghiệm phân biệt khác 2
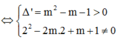
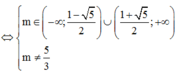
Giả sử x B ; x C ( x B < x C ) là 2 nghiệm phân biệt của phương trình (*).
Để hai điểm B, C một điểm nằm trong một điểm nằm ngoài đường tròn x2 + y2 = 1
TH1: ![]()
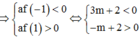
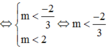
TH2: ![]()
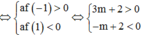
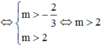
Kết hợp điều kiện ta có: 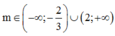
Lại có m ∈ [–10;100]
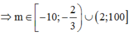
=> Có 108 giá trị m nguyên thỏa mãn yêu cầu bái toán

Đáp án là B.
+ Hàm số có 3 cực trị khi − 2 m + 1 < 0 ⇔ m > − 1. (1)
+ y ' = 4 x 3 − 4 m + 1 x = 0 ⇔ x = 0 x = ± m + 1
Các điểm cực trị A, B, C của đồ thị là: A 0 ; m ;
B m + 1 ; − m 2 − m − 1 ; C − m + 1 ; − m 2 − m − 1
+ O A = B C ⇔ m = 2 m + 1 ⇔ m 2 − 4 m − 4 = 0
⇔ m = 2 ± 2 2 .
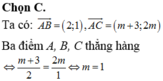

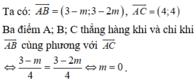



Theo công thức tọa độ trọng tâm:
\(\left\{{}\begin{matrix}x_G=\frac{1-2m+2m+3m-1}{3}=m\\y_G=\frac{4m+1-m+0}{3}=m+\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow x_G-y_G=-\frac{1}{3}\)
\(\Leftrightarrow3x_G-3y_G+1=0\)
\(\Rightarrow\) G nằm trên đường thẳng \(3x-3y+1=0\)
Cảm ơn bạn nhiều nha