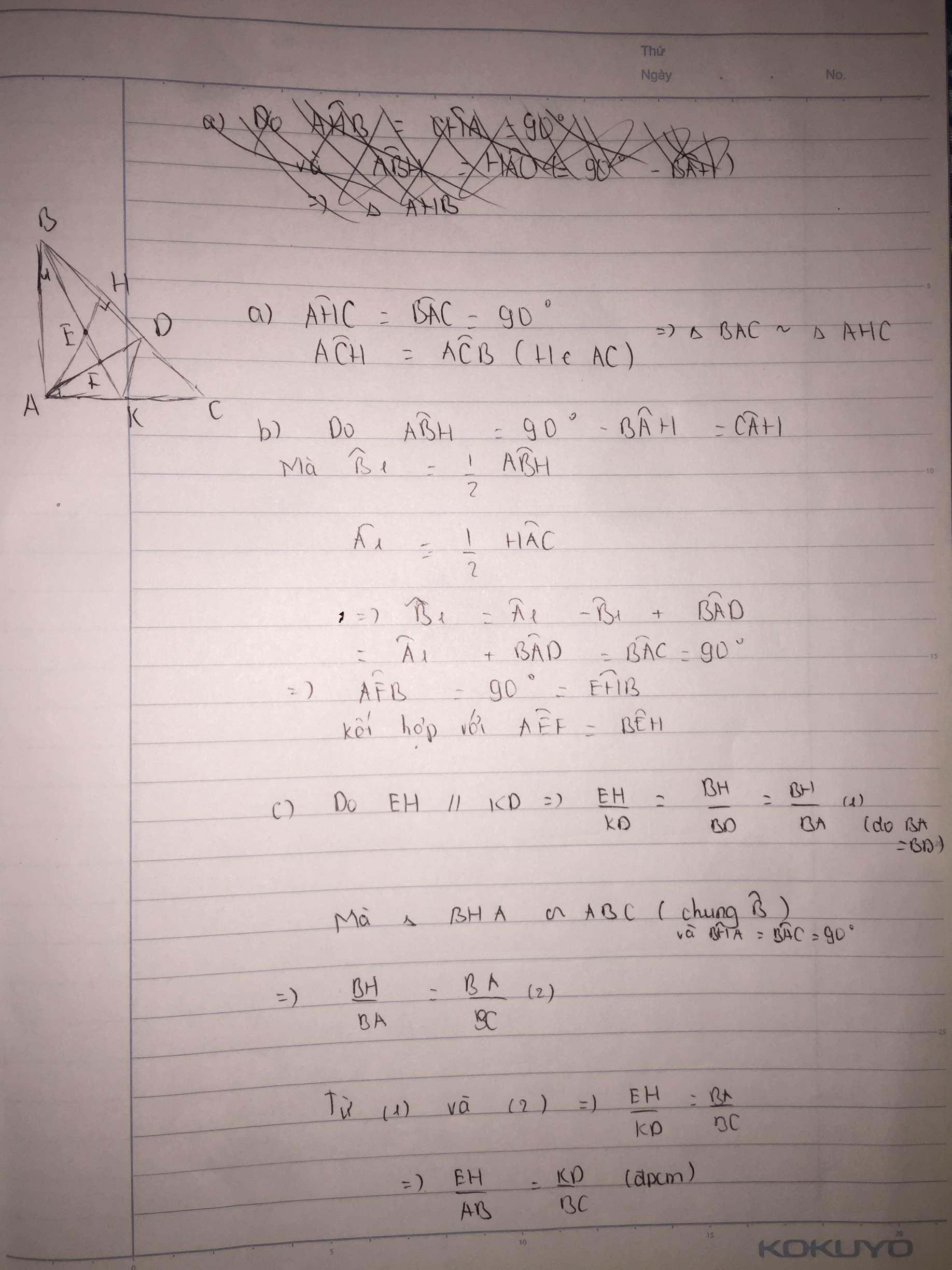Cho \(\Delta ABC\) \(\left(\widehat{BAC}=90^o\right)\), BD là phân giác \(\widehat{ABC}\left(D\in AC\right)\) kẻ\(AH\perp BD\) tại H, đường thẳng AH cắt BC tại M
a) Chứng minh \(\Delta ADH\) đồng dạng với \(\Delta BDA\), \(\Delta BHM\) đồng dạng với \(\Delta BAD\)
b) Qua điểm D kẻ đường thẳng song song với AM cắt tia đôi của tia AB tại P
Chứng minh \(AP.BD=AD.DP\)
c) Gọi N là giao điểm của PD và BC. Chứng minh \(\frac{1}{BD^2}=\frac{DC}{BC.BN.DM}\)