Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: \(S_{DEF}=\dfrac{EH\cdot DF}{2}=\dfrac{ED\cdot EF}{2}\)
nên \(EH\cdot DF=ED\cdot EF\)
b: \(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
c: Xét ΔDEF vuông tại E có EH là đường cao
nên \(EF^2=DF\cdot HF\)
d: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
Xét ΔEMN và ΔEFD có
EM/EF=EN/ED
góc MEN chung
Do đo: ΔEMN đồng dạng với ΔEFD
a: Xét ΔDEF vuông tại E cso EH là đường cao
nên \(EH\cdot DF=ED\cdot EF\)(hệ thức lượng)
\(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{ED\cdot EF}{DF}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
b: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
Xét ΔEMN vuông tại E và ΔEFD vuông tại E có
EM/EF=EN/ED
Do đó ΔEMN\(\sim\)ΔEFD
Câu 1:
a: \(S_{EDF}=\dfrac{EH\cdot DF}{2}=\dfrac{ED\cdot EF}{2}\)
nên \(EH\cdot DF=ED\cdot EF\)
\(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{ED\cdot EF}{FD}=12\left(cm\right)\)
b: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
=>ΔEMN\(\sim\)ΔEFD
a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó:ΔDHE=ΔDHF
b: EF=8cm nên HE=4cm
=>DH=3cm
c: Xét ΔDMH vuông tại M và ΔDNH vuông tại N có
DH chung
\(\widehat{MDH}=\widehat{NDH}\)
Do đó:ΔDMH=ΔDNH
Suy ra: HM=HN
\(\text{a)}\text{Vì }\Delta DEF\text{ cân tại D}\)
\(\Rightarrow DE=DF\)
\(\widehat{E}=\widehat{F}\)
\(\text{Xét }\Delta DHE\text{ và }\Delta AHF\text{ có:}\)
\(DE=DF\left(cmt\right)\)
\(BH\text{ chung}\)
\(\widehat{E}=\widehat{F}\left(cmt\right)\)
\(\Rightarrow\Delta DHE=\Delta DHF\left(c-g-c\right)\)
\(\Rightarrow EH=HF\text{(hai cạnh tương ứng)}\)
\(\text{b)}\text{Vì }EH=HF\left(cmt\right)\)
\(\Rightarrow EH=\dfrac{EF}{2}=\dfrac{8}{2}=4\left(cm\right)\)
\(\text{Xét }\Delta DEH\text{ có:}\)
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH^2=DE^2-EH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow DH^2=5^2-4^2=25-16=9\left(cm\right)\)
\(\Rightarrow DH=\sqrt{9cm}=3\left(cm\right)\)
\(\text{c)Xét }\Delta HMD\text{ và }\Delta HND\text{ có:}\)
\(DH\text{ chung}\)
\(\widehat{D_1}=\widehat{D_2}\left(\Delta DHE=\Delta DHF\right)\)
\(\widehat{DMH}=\widehat{DNH}=90^0\)
\(\Rightarrow\Delta HMD=\Delta HND\left(ch-cgv\right)\)
\(\Rightarrow HM=HN\text{( hai cạnh tương ứng)}\)
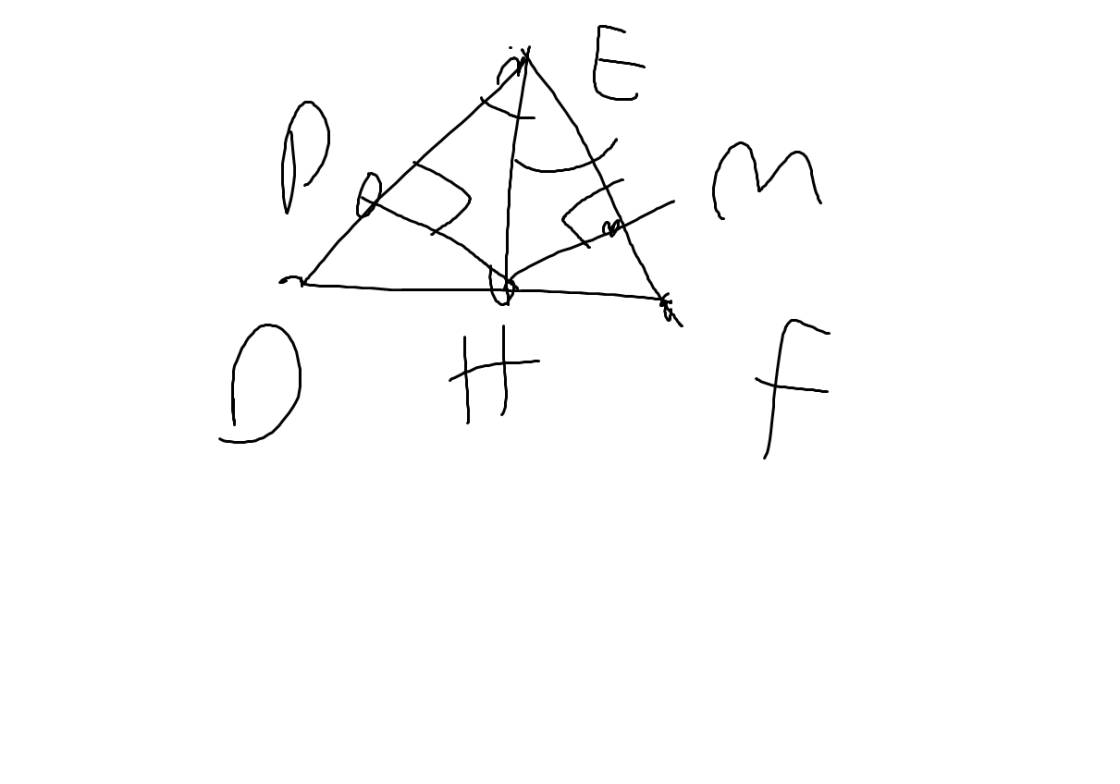
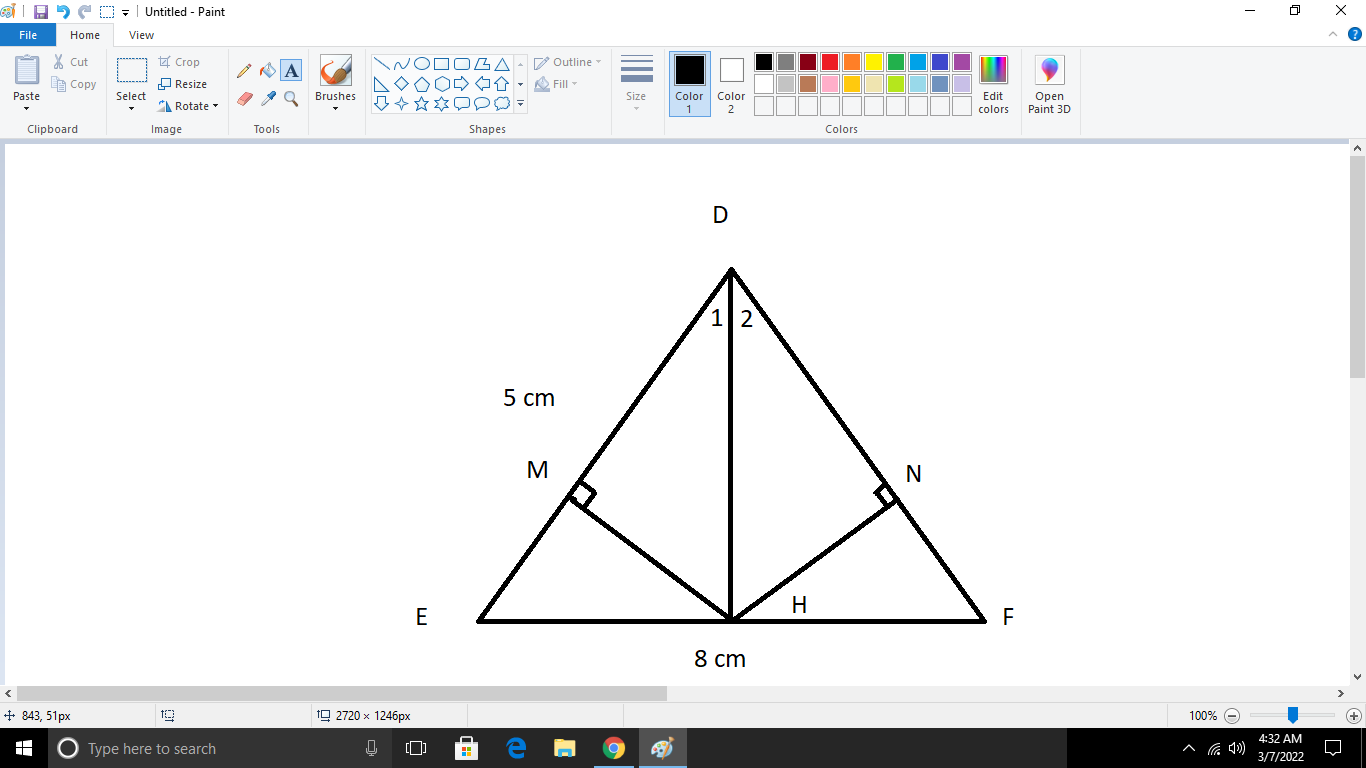
Bài làm
a) Xét tam giác DEH và tam giác DEF có:
\(\widehat{DHE}=\widehat{DEF}\left(=90^0\right)\)
\(\widehat{D}\) chung
=> Tam giác DEH ~ Tam giác DEF ( g - g )
=> \(\frac{DE}{DF}=\frac{HE}{EF}\)
\(\Rightarrow DE.EF=DF.EH\) ( đpcm )
b) Xét tam giác DEF vuông tại E có:
DF2 = DE2 + EF2
hay DF2 = 152 + 202
=> DF2 = 225 + 400
=> DF2 = 625
=> DF = 25 ( cm )
Vì tam giác DEH ~ Tam giác DEF ( cmt )
=> \(\frac{DH}{DE}=\frac{DE}{DF}\)
hay \(\frac{DH}{15}=\frac{15}{25}\Rightarrow DH=9\left(cm\right)\)
Ta có: DH + HF = DF
hay 9 + HF = 25
=> HF = 16 ( cm )
c) Xét tam giác HEF và tam giác EDF có:
\(\widehat{EHF}=\widehat{DEF}\left(=90^0\right)\)
\(\widehat{F}\) chung
=> Tam giác HEF ~ Tam giác EDF ( g - g )
=> \(\frac{EF}{DF}=\frac{HF}{EF}\Rightarrow EF^2=DF.HF\) ( đpcm )