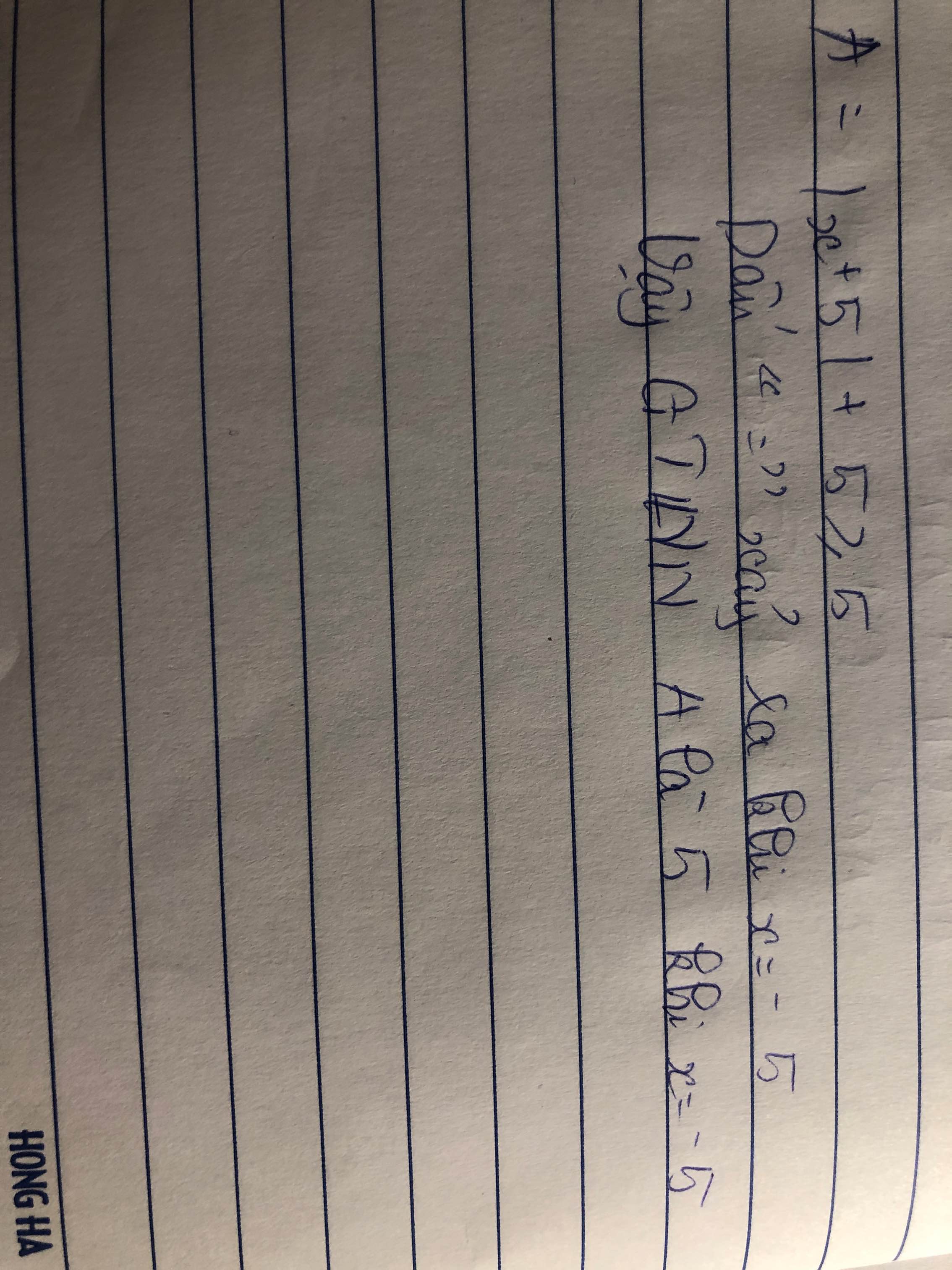Tìm giá trị lớn nhất hoặc nhỏ nhất của các biểu thức sau :
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
21 tháng 6 2022
\(A=\left(x-4\right)^2+1\)
Ta có: \(\left(x-4\right)^2\ge0\Rightarrow\left(x-4\right)^2+1\ge1\Rightarrow A\ge1\)
\(A_{min}=1\Leftrightarrow x=4\)
\(B=\left|3x-2\right|-5\)
Ta có: \(\left|3x-2\right|\ge0\Rightarrow\left|3x-2\right|-5\ge-5\Rightarrow B\ge-5\)
\(B_{min}=-5\Leftrightarrow x=\dfrac{2}{3}\)
\(C=5-\left(2x-1\right)^4\)
Ta có: \(\left(2x-1\right)^4\ge0\forall x\Rightarrow-\left(2x-1\right)^4\le0\forall x\Rightarrow5-\left(2x-1\right)^4\le5\Rightarrow C\le5\)
\(C_{max}=5\Leftrightarrow x=\dfrac{1}{2}\)
\(D=-3\left(x-3\right)^2-\left(y-1\right)^2-2021\)
Ta có: \(\left\{{}\begin{matrix}-3\left(x-3\right)^2\le0\forall x\\-\left(y-1\right)^2\le0\forall y\end{matrix}\right.\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2\le0\forall x,y\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2-2021\le-2021\Rightarrow D\le-2021\)
\(D_{max}=-2021\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
\(E=-\left|x^2-1\right|-\left(x-1\right)^2-y^2-2020\)
\(=-\left|\left(x-1\right)\left(x+1\right)\right|-\left(x-1\right)^2-y^2-2020\)
Ta có: \(\left\{{}\begin{matrix}\left|\left(x-1\right)\left(x+1\right)\right|\ge0\forall x\Rightarrow-\left|\left(x-1\right)\left(x+1\right)\right|\le0\\\left(x-1\right)^2\ge0\forall x\Rightarrow-\left(x-1\right)^2\le0\\y^2\ge0\Rightarrow-y^2\le0\end{matrix}\right.\Rightarrow E\le-2020\)
\(E_{max}=-2020\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
PT
1
CM
1 tháng 4 2019
C = 5 x - x 2 = - x 2 - 5 x = - x 2 - 2 . 5 / 2 x + 5 / 2 2 - 5 / 2 2 = - x - 5 / 2 2 - 25 / 4 = - x - 5 / 2 2 + 25 / 4 V ì - x - 5 / 2 2 ≤ 0 ⇒ - x - 5 / 2 2 + 25 / 4 ≤ 25 / 4
Suy ra: C ≤ 25/4 .
C = 25/4 khi và chỉ khi x - 5/2 = 0 suy ra x = 5/2
Vậy C = 25/4 là giá trị lớn nhất tại x = 5/2 .
PT
1
CM
3 tháng 3 2019
2 x 2 + 10 - 1 = 2 x 2 + 5 x - 1 / 2 B = 2 x 2 + 2 . 5 / 2 x + 5 / 2 2 - 5 / 2 2 - 1 / 2 = 2 x + 5 / 2 2 - 25 / 4 - 2 / 4 = 2 x + 5 / 2 2 - 27 / 2 = 2 x + 5 / 2 2 - 27 / 2 V ì x + 5 / 2 2 ≥ 0 n ê n 2 x + 5 / 2 2 ≥ 0 ⇒ 2 x + 5 / 2 2 - 27 / 2 ≥ - 27 / 2
Suy ra: B ≥ - 27/2 .
B= -27/2 khi và chỉ khi x + 5/2 = 0 suy ra x = -5/2
Vậy B = -27/2 là giá trị nhỏ nhất tại x = - 5/2
PT
1
CM
15 tháng 1 2018
Ta có: A = x 2 - 6 x + 11 = x 2 - 2 . 3 x + 9 + 2 = x - 3 2 + 2
Vì x - 3 2 ≥ 0 nên x - 3 2 + 2 ≥ 2
Suy ra: A ≥ 2.
A = 2 khi và chỉ khi x - 3 = 0 suy ra x = 3
Vậy A = 2 là giá trị nhỏ nhất của biểu thức tại x =3.
AH
Akai Haruma
Giáo viên
15 tháng 6 2023
Đề đọc khó hiểu. Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.
HD
2
27 tháng 7 2017
Vì |x-3|>/=0
=>|x-3|+1>/=0+1
=> A>/=1
dấu "=" xảy ra khi<=>|x-3|=0
x-3=0
x=0+3
x=3
Vậy min A=1
Khi x=3
27 tháng 7 2017
A = | x - 3 | + 1
Vì | x - 3 | \(\ge0\forall x\)
=> | x - 3 | + 1 \(\ge1\forall x\)
=> A \(\ge1\forall x\)
=> A = 1 <=> | x - 3 | = 0
<=> x - 3 = 0
<=> x = 3
Vậy A min = 1 khi x = 3
PT
1
CM
24 tháng 10 2017
B = 9 x - 3 x 2 = 3 3 x - x 2 = 3 9 / 4 - 9 / 4 + 2 . 3 / 2 x - x 2
= 3 9 / 4 - 9 / 4 - 3 / 2 x + x 2
= 3 9 / 4 - 3 / 2 x - x 2 = 27 / 4 - 3 / 2 - x 2
Vì 3 / 2 - x 2 ≥ 0 với mọi x
⇒ B = 27/4 − 3 / 2 - x 2 ≤ 27/4 do đó giá trị lớn nhất của B bằng 27/4 tại x = 3/2
PT
1
CM
30 tháng 7 2018
A = 2 x 2 - 8 x - 10
= 2 x 2 - 4 x + 4 - 18 = 2 x - 2 2 - 18
Do 2 x - 2 2 ≥ 0 với mọi x ⇒ 2 x - 2 2 – 18 ≥ −18
A = -18 khi và chỉ khi x - 2 = 0 hay x = 2
Do đó giá trị nhỏ nhất của biểu thức A bằng -18 tại x = 2
NM
4
16 tháng 7 2021
Với mọi x ta có :
\(\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|+5\ge0\)
\(\Leftrightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy..
NQ
1