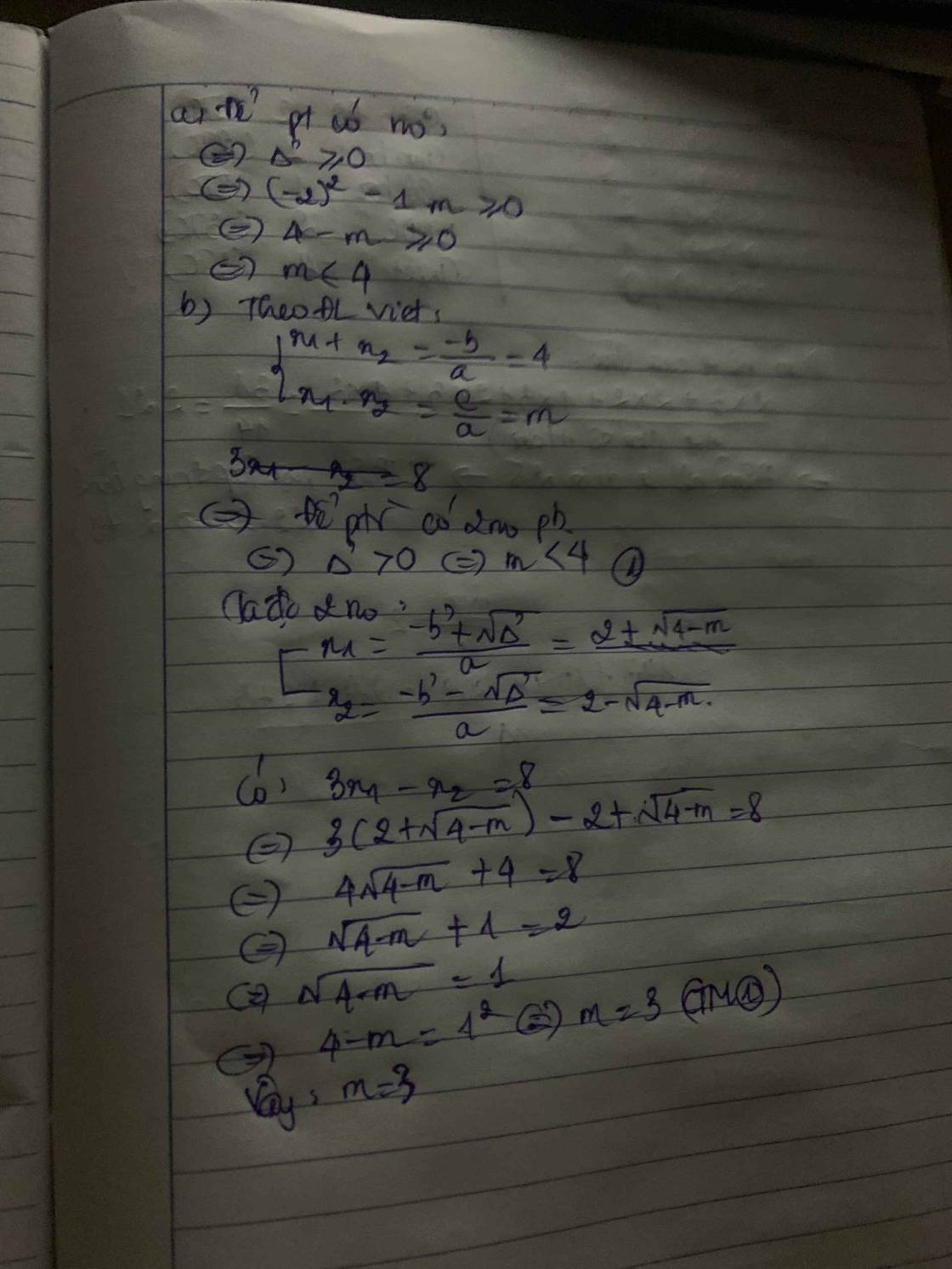Tìm m để pt sau có nghiệm \(x^4-4x^2+4mx-m^2=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 1 2022
a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4
LL
0
AH
Akai Haruma
Giáo viên
13 tháng 7 2020
Bài 5:
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m-1)^2-m^2\geq 0$
$\Leftrightarrow (m-1-m)(m-1+m)\geq 0$
$\Leftrightarrow 1-2m\geq 0\Leftrightarrow m\leq \frac{1}{2}(*)$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2\end{matrix}\right.\)
Khi đó:
$(x_1-x_2)^2+6m=x_1-2x_2$
$\Leftrightarrow (x_1+x_2)^2-4x_1x_2+6m=(x_1+x_2)-3x_2$
$\Leftrightarrow 4(m-1)^2-4m^2+6m=2(m-1)-3x_2$
$\Leftrightarrow 4m-6=3x_2$
$\Leftrightarrow x_2=\frac{4}{3}m-2$
$x_1=2(m-1)-x_2=\frac{2}{3}m$
Suy ra:
$x_1x_2=m^2$
$\Leftrightarrow \frac{2}{3}m(\frac{4}{3}m-2)=m^2$
$\Leftrightarrow m(8m-12-9m)=0$
$\Leftrightarrow m(-m-12)=0$
$\Leftrightarrow m=0$ hoặc $m=-12$. Theo $(*)$ ta thấy 2 giá trị này đều thỏa mãn.
AH
Akai Haruma
Giáo viên
13 tháng 7 2020
Bài 4:
Để pt có 2 nghiệm thì $\Delta'=4-2(2m^2-1)\geq 0$
$\Leftrightarrow m^2-1\leq 0\Leftrightarrow -1\leq m\leq 1$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=\frac{2m^2-1}{2}\end{matrix}\right.\)
Khi đó:
$2x_1^2+4mx_2+2m^2-1\geq 0$
$\Leftrightarrow (2x_1^2-4mx_1+2m^2-1)+4mx_1+4mx_2\geq 0$
$\Leftrightarrow 0+4m(x_1+x_2)\geq 0$
$\Leftrightarrow 4m. 2\geq 0$
$\Leftrightarrow m\geq 0$
Kết hợp với điều kiện $-1\leq m\leq 1$ suy ra $0\leq m\leq 1$ thì ycđb được thỏa mãn.
MH
1
8 tháng 8 2023
Δ=(-4m)^2-4(4m^2-m+2)
=16m^2-16m^2+4m-8=4m-8
Để phương trình có hai nghiệm phân biệt thì 4m-8>0
=>m>2
|x1-x2|=2
=>\(\sqrt{\left(x_1-x_2\right)^2}=2\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{\left(4m\right)^2-4\left(4m^2-m+2\right)}=2\)
=>\(\sqrt{16m^2-16m^2+4m-8}=2\)
=>\(\sqrt{4m-8}=2\)
=>4m-8=4
=>4m=12
=>m=3(nhận)
HN
16 tháng 3 2022
Kiểm tra giúp mình yêu cầu thứ nhất nhé!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (m2-1)x+2=m-1 nhận x=2 là nghiệm.
Giải: Thế x=2 vào phương trình đã cho, ta suy ra (m2-1).2+2=m-1 (vô nghiệm).
Không có giá trị nào của m để phương trình đã cho nhận x=2 là nghiệm. -Hết-".
Thế x=-1 vào phương trình đã cho, ta suy ra 3.(-1)2+4m.(-1)=8 \(\Rightarrow\) m=-5/4.
Bạn xem giúp mình yêu cầu cuối cùng nha!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (2m+3)x-5=(m+2)-x có nghiệm là x=3.
Giải: Thế x=3 vào phương trình đã cho, ta suy ra (2m+3).3-5=(m+2)-3 \(\Rightarrow\) m=-1. -Hết-".
Y
4 tháng 5 2023
\(m=0\) là okee rồi nè
còn \(x_1=x_2\) thì như sau :
\(\Leftrightarrow x_1-x_2=0\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=0^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\)
Tới đây rồi áp dụng cái Vi-ét vào là được m còn lại nhe.