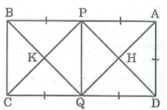
Cho hình vuông ABCD có cạnh là x. Gọi H và K thứ tự là trung điểm AB; BC. Biết CH cắt DK tại M. Tính diện tích tam giác MCD theo x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 5 2020
Xét 2 tam giác: Tam giác BHC và Tam giác CKD có:
\(\hept{\begin{cases}HB=KC\left(=\frac{AB}{2}=\frac{BC}{2}\right)\\\widehat{HBC}=\widehat{DCK}\\BC=CD\left(gt\right)\end{cases}}\)
=>Tam giác BHC= Tam giác CKD(c.g.c)
=>\(\widehat{HCB}=\widehat{KDC}\)
Mà ta có: \(\widehat{KDC}+\widehat{DKC}=90^0\)
NÊN \(\widehat{HCB}+\widehat{DKC}=90^0\)
=>\(\widehat{KMC}=90^0\)
=> Tam giác KMC vuông tại M.
Bài này dài nên tiếp theo mk sẽ tóm tắt thôi nhé!
Vì BC=x =>KC=BC/2=x/2
Từ đó theo định lý Py-ta-go ta tính đc \(HC=\frac{\sqrt{5}x}{2}\)
Xét tam giác CMK và tam giác CBH đồng dang với nhau theo th (g.g) vì có góc HCB chung và góc HBC bằng góc KMC vì cùng bằng 90 độ
=>\(\frac{MC}{BC}=\frac{KC}{HC}\)
Thay BC=x, KC=x/2 và \(HC=\frac{\sqrt{5}x}{2}\) vào tính thì ta tính đc \(MC=\frac{x}{\sqrt{5}}\)
Áp dụng tiếp đinh lý Py-ta-go trong tam giác vuông MDC có DC=x, \(MC=\frac{x}{\sqrt{5}}\)
=> \(MD=\frac{2x}{\sqrt{5}}\)
=> Diện tích tam giác MCD là: \(S=\frac{MD.MC}{2}=\frac{2x^2}{10}\)
Chúc bạn học tốt!
CM
25 tháng 3 2017
* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = 1/2 .AB (gt)
QD = 1/2 CD (gt)
AB= CD (vì ABCD là hình chữ nhật)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: ∠ A = 90 0 (vì tứ giác ABCD là hình chữ nhật)
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (t/chất hình vuông) ⇒ ∠ (PHQ) = 90 0 (1)
HP = HQ (t/chất hình vuông)
* Xét tứ giác PBCQ, ta có: AB // CD hay BP //CQ
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
AB = CD do ABCD là hình chữ nhật
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Lại có: ∠ B = 90 0 (vì ABCD là hình chữ nhật) suy ra tứ giác PBCQ là hình chữ nhật
PB = BC ( vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (t/chất hình vuông) ⇒ ∠ (PKQ) = 90 0 (2)
PD là tia phân giác ∠ (APQ) ( t/chất hình vuông)
PC là tia phân giác ∠ (QPB) (t/chất hình vuông)
Suy ra: PD ⊥ PC (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ (HPK) = 90 0 (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
16 tháng 11 2021
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
CM
29 tháng 10 2019
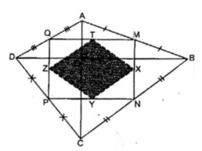
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.
22 tháng 2 2022
Xét tứ giác APQD có
AP//QD
AP=QD
DO đó: APQD là hình bình hành
mà AP=AD
nên APQD là hình thoi
mà \(\widehat{PAD}=90^0\)
nên APQD là hình vuông
=>Hai đường chéo AQ và PD vuông góc với nhau tại trung điểm của mỗi đường và bằng nhau
=>H là trung điểm chung của AQ và PD và AQ vuông góc PD tại H
Xét tứ giác BPQC có
BP//QC
BP=QC
Do đó: BPQC là hình bình hành
mà BP=BC
nên BPQC là hình thoi
=>BQ vuông góc với CP tại trung điểm của mỗi đường
hay K là trung điểm chung của BQ và CP
Xét ΔDPC có
PQ là đường trung tuyến
PQ=CD/2
Do đó: ΔDPC vuông tại P
Xét tứ giác PHQK có
\(\widehat{PHQ}=\widehat{PKQ}=\widehat{HPK}=90^0\)
Do đó: PHQK là hình chữ nhật
mà PH=QH
nên PHQK là hình vuông
24 tháng 10 2021
TL
Mik ko có hình cả sai mik sorry nha
Độ dài cạnh AM là:
8:2=4(cm)
Độ dài cạnh AM cũng chính là độ dài của cạnh MB,BN,NC.
Diện tích hình tam giác AMD là :
4x8:2=16(cm2)
Diện tích hình tam giác NCD là:
8x4:2=16(cm2)
Diện tích hình tam giác MBN là:
4x4:2=8(cm2)
Diện tích hình vuông ABCD là :
8x8=64(dm2)
Diện tích hình tam giác MND là :
64-(8+16 + 16)=24(dm2)
Đáp số:24dm2
Hok tốt