 Làm giúp em hai bài 1,2 ạ
Làm giúp em hai bài 1,2 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)

\(a,\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m-2\right)\ge0\\ \Leftrightarrow m^2-3m+3\ge0\\ \Leftrightarrow\left(m-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge0\left(\text{luôn đúng}\right)\)
Vậy PT có 2 nghiệm pb với mọi m
\(b,\Leftrightarrow0< x_1< x_2\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\left(m-1\right)>0\\m-2>0\end{matrix}\right.\Leftrightarrow m>2\\ c,\text{Thay }x=2\Leftrightarrow4-4\left(m-1\right)+m-2=0\\ \Leftrightarrow m=2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\\ d,\text{Viét: }\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m-2\end{matrix}\right.\\ x_1^2+x_2^2=8\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\\ \Leftrightarrow4\left(m-1\right)^2-2\left(m-2\right)=8\\ \Leftrightarrow4m^2-10m=0\\ \Leftrightarrow m\left(2m-5\right)=0\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{5}{2}\end{matrix}\right.\)

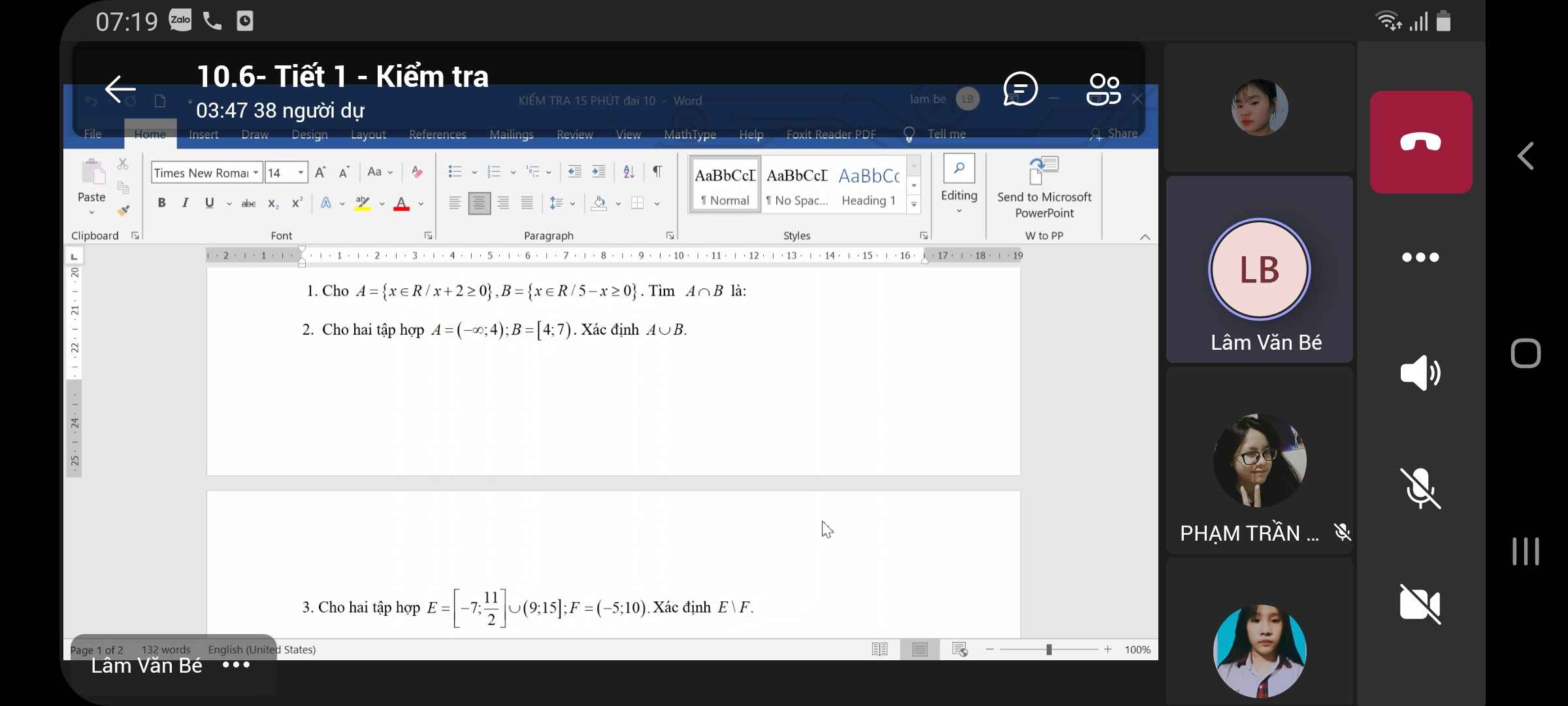
\(1,\\ x+2\ge0\Leftrightarrow x\ge-2\)
\(\Leftrightarrow A=\)\([-2;+\infty)\)
\(5-x\ge0\Leftrightarrow x\le5\)
\(\Leftrightarrow B=\)\((-\infty;5]\)
\(\Leftrightarrow A\cap B=\left[-2;5\right]\)
\(2,A\cup B=\varnothing\)

Bài 1.
a) Ta có
\(f\left(x\right)=9-x^5+4x-2x^3+x^2-7x^4\\ f\left(x\right)=-x^5-7x^4-2x^3+x^2+4x+9\)
Lại có:
\(g\left(x\right)=x^5-9+2x^2+7x^4+2x^3-3x\\ g\left(x\right)=x^5+7x^4+2x^3+2x^2-3x-9\)
b) \(h\left(x\right)=f\left(x\right)+g\left(x\right)\)
\(h\left(x\right)=\left(-x^5+x^5\right)+\left(-7x^4+7x^4\right)+\left(-2x^3+2x^3\right)+\left(x^2+2x^2\right)+\left(4x-3x\right)+\left(9-9\right)\)
\(h\left(x\right)=3x^2+x\)
c) \(h\left(x\right)=0\)
\(3x^2+x=0\)
\(x\left(3x+1\right)=0\)
TH1: \(x=0\)
TH2: \(3x+1=0\) hay \(x=-\dfrac{1}{3}\)
Vậy nghiệm của \(h\left(x\right)\) là \(x=0;x=-\dfrac{1}{3}\)
Bài 2.
a) Ta có \(\left\{{}\begin{matrix}A\left(x\right)=6x^3+5x^2\\B\left(x\right)=x^3-x^2\\C\left(x\right)=-2x^3+4x^2\end{matrix}\right.\)
\(D\left(x\right)=A\left(x\right)+B\left(x\right)-C\left(x\right)\)
\(D\left(x\right)=\left(6x^3+x^3-\left(-2x^3\right)\right)+\left(5x^2-x^2-4x^2\right)\)
\(D\left(x\right)=9x^3\)
b) \(D\left(x\right)=0\)
\(9x^3=0\\ x^3=0\\ x=0\)
Vậy nghiệm của đa thức \(D\left(x\right)\) là \(x=0\).


Đăng tách ra bạn nhé
Vì AD là pg \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{5}{4}=\dfrac{3}{DC}\Rightarrow DC=\dfrac{12}{5}cm\)
BC = DC + DB = 12/5 + 3 = 27/5 cm
chọn B

Bài 1.
a,Vì \(\dfrac{a}{b}>1\)=>a<b
Với m∈N* Ta có
\(am> bm\)=>\(am+ab> bm+ab\)=>\(a\left(b+m\right)> b\left(a+m\right)\)=>\(\dfrac{a}{b}>\dfrac{a+m}{b+m} \)
b, Vì \(\dfrac{a}{b}< 1\)=>a<b
Với m∈N* =>
\(am< bm\)=>\(am+ab< bm+ab\)=>\(a\left(b+m\right)< b\left(a+m\right)\)=>\(\dfrac{a}{b}<\dfrac{a+m}{b+m} \)
Tự áp dụng cho bài 2 nhé bạn :)

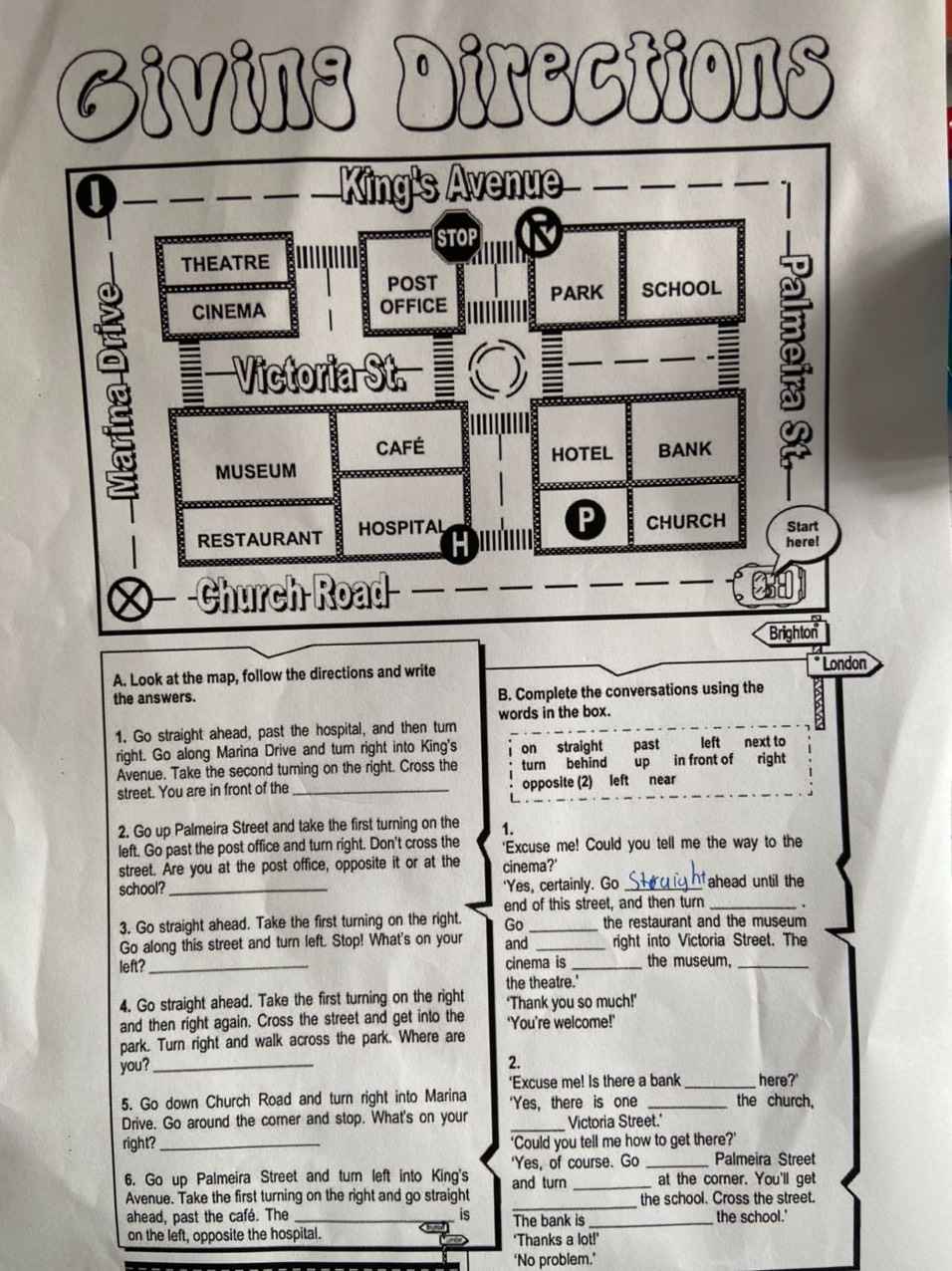 giúp em hai bài ở dưới ạ bài 1,2 ạ
giúp em hai bài ở dưới ạ bài 1,2 ạ 





gbsgebhbhbgeghegfegegjkgbwjg