Question

[Ng.H.Bảo Khánh]

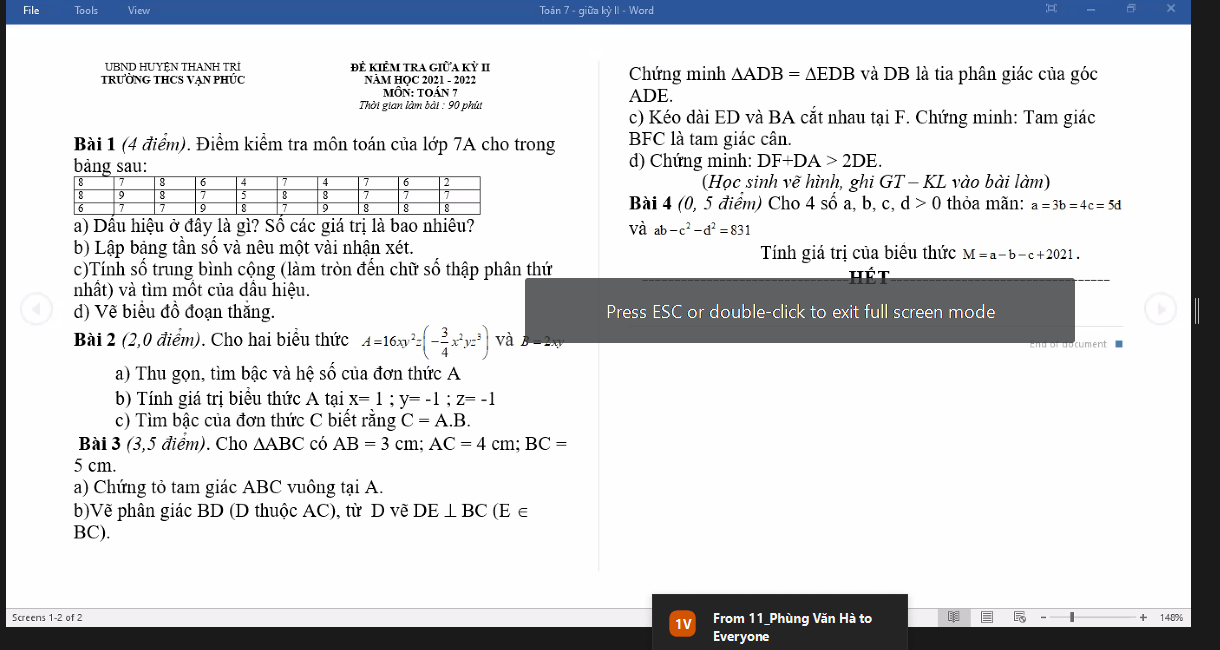
Giúp mình với

Answer 1

[Xyz OLM]

a) Ta có \(\frac{\sqrt{x}}{x-1}+\frac{\sqrt{x}}{\sqrt{x}-1}=\frac{\sqrt{x}+\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{x-1}\)

\(\frac{2}{x}-\frac{2-x}{x\sqrt{x}+x}=\frac{2\left(\sqrt{x}+1\right)-2+x}{x\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{x\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+1\right)}\)

Khi đó P = \(\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{x-1}:\frac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{x\left(\sqrt{x}+1\right)}{x-1}=\frac{x}{\sqrt{x}-1}\)

b) Để P = -1/2 

=> \(\frac{x}{\sqrt{x}-1}=-\frac{1}{2}\)

=> \(2x+\sqrt{x}-1=0\)

<=> \(\left(2\sqrt{x}-1\right)\left(\sqrt{x}+1\right)=0\)

<=> \(2\sqrt{x}-1=0\)

<=> \(x=\frac{1}{4}\)(tm)

Vậy x = 1/4 

c) Nhận thấy \(\sqrt{P}\)đạt MIN khi P \(>0\Rightarrow x>1\)

Khi đó \(P=\frac{x}{\sqrt{x}-1}=\frac{4\sqrt{x}-4+x-4\sqrt{x}+4}{\sqrt{x}-1}=4+\frac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}\ge4\)

=> Min \(\sqrt{P}=2\)

Dấu "=" xảy ra <=> x = 4 

Vậy Min \(\sqrt{P}\)= 2 khi x = 4

Answer 2

[Lê Song Phương]

\(P=\left(\frac{\sqrt{x}}{x-1}+\frac{\sqrt{x}}{\sqrt{x}-1}\right):\left(\frac{2}{x}-\frac{2-x}{x\sqrt{x}+x}\right)\)\(\left(x>0;x\ne1\right)\)

\(P=\left[\frac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\frac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]\)\(:\left[\frac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\frac{2-x}{x\left(\sqrt{x}+1\right)}\right]\)

\(P=\left[\frac{\sqrt{x}+x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]:\left[\frac{2\sqrt{x}+2-2+x}{x\left(\sqrt{x}+1\right)}\right]\)

\(P=\frac{\left(x+2\sqrt{x}\right)x\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+2\sqrt{x}\right)}\)

\(P=\frac{x}{\sqrt{x}-1}\)

b) Để \(P=-\frac{1}{2}\)thì \(\frac{x}{\sqrt{x}-1}=\frac{-1}{2}\Rightarrow2x=1-\sqrt{x}\Leftrightarrow2x+\sqrt{x}-1=0\Leftrightarrow2x+2\sqrt{x}-\sqrt{x}-1=0\)

\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}+1\right)-\left(\sqrt{x}+1\right)=0\Leftrightarrow\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}+1=0\\2\sqrt{x}-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=-1\left(vôlí\right)\\\sqrt{x}=\frac{1}{2}\end{cases}\Leftrightarrow}x=\frac{1}{4}\left(nhận\right)}\)

Vậy để P = -1/2 thì x = 1/4