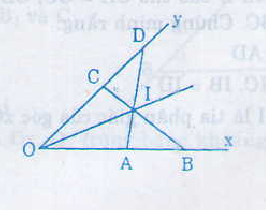
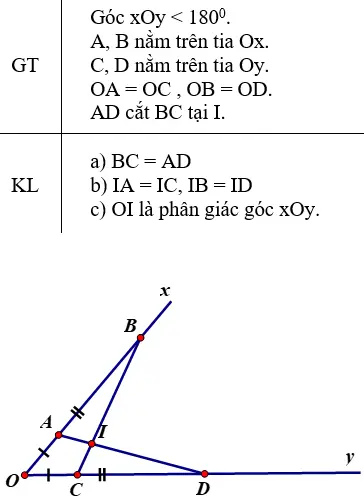
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai
điểm C và D sao cho OA =OC ,OB =OD , . Gọi I là giao điểm của hai đoạn thẳng AD và
BC. Chứng minh rằng:
a) BC= AD ;
b) IA =IC, IB =ID , ;
c) Tia OI là tia phân giác của góc xOy .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 3 2019
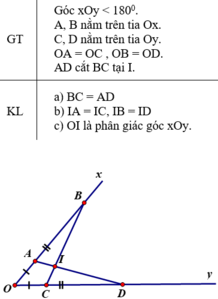
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
CM
3 tháng 1 2019
Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
CM
30 tháng 12 2018
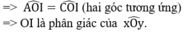
- ΔAOD = ΔCOB
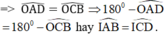
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
- Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
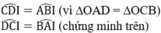
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
WJ
20 tháng 6 2016
HÌnh bạn tự vẽ (vẽ góc nhọn)
a) Xét \(\Delta COB\)và \(\Delta AOD\)ta có:
OB=OA
Góc xOy chung
OC=OD
\(\Rightarrow\Delta COB=\Delta AOD\left(c-g-c\right)\)
\(\Rightarrow BC=AD\)(cặp cạnh tương ứng)
b) Bạn ghi lại, đề bài sai nên phần c chưa làm đc!
19 tháng 4 2017
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB =>
=> (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
( ∆AOD = ∆COB)
(chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=>
=> OI là phân giác của
J
8 tháng 4 2021
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
b) – ΔAOD = ΔCOB
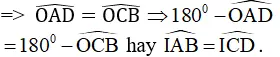
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
– Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
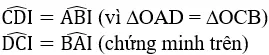
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
c) Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
19 tháng 4 2017
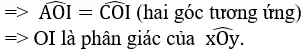
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB =>
=> (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
( ∆AOD = ∆COB)
(chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=>
=> OI là phân giác của
19 tháng 4 2017
Hướng dẫn:
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
ˆxOyxOy^ là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB => ˆAOD=ˆOCBAOD^=OCB^
=> ˆBAI=ˆDCIBAI^=DCI^ (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
ˆDCI=ˆABIDCI^=ABI^ ( ∆AOD = ∆COB)
ˆBAI=ˆDCIBAI^=DCI^ (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> ˆCOI=ˆAOICOI^=AOI^
=> OI là phân giác của ˆxOy
CM
17 tháng 10 2017
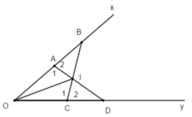
+ Giả sử A nằm giữa hai điểm O và B; C nằm giữa hai điểm O và D
Do đó ta có: OA + AB = OB; OC + CD = OD
Mà OA = OC; OB = OD (gt)
Nên AB = CD
+ Xét tam giác OAD và tam giác OCB có:
OA = OC; OB = OD (gt)
x O y ^ góc chung
Do đó: Δ O A D = Δ O C B (c – g – c)
Đáp án D
29 tháng 3 2018
a)Xét tam giác AOD VÀ COB có AO=OC ,OB=OD ,chung góc O=> tam giác AOD =tam giác COB(cgc)=>AD=BC
29 tháng 3 2018
b) Ta có OA=OC,OB=OC=> AB=CD.
Tam giác AOD=tg COB=> góc OAD =góc BCO góc
Và ADO=gócCBO(2 góc tương ứng).
Mà góc ABI + góc CBO=180 độ(kề bù)
góc CDI+góc ADO=180 độ (kề bù)
=> Góc CBO=ADO
Xét tg ABI và tg CDI có AB= CD(cm trên),gics CBO= góc ADO,góc OAC= BCO=> tg ABI=th CDI => AI=CI,BI=Di
hoang phuong anh