Cho hình vuông ABCD có cạnh bằng a. Gọi E;F lần lượt là trung điểm của các cạnh AB,BC.M là giao điểm của các cạnh CE và DF. a) Chứng minh CE Vuông góc với DF. b) Chứng minh \(\Delta MAD\)cân. c) Tính diện tích \(\Delta MDC\)theo a.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
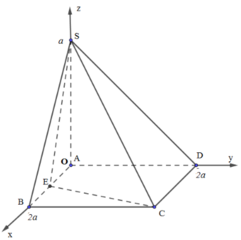
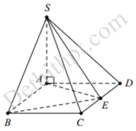
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
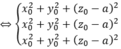
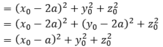
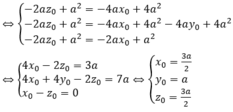
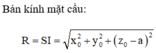
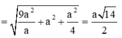
![]()


Đáp án A
Hình chóp SABE có cạnh bên S A ⊥ đáy (ABE) ta có công thức tính bán kính mặt cầu của hình chóp dạng này là R = R d 2 + h 2 2 ( với R d là bán kính đường tròn ngoại tiếp đáy và h là chiều cao hình chóp )
Ta có: h = S A = a ; d t A B E = 1 2 E H . A B = a 2 2
A E = B E = a 2 + a 2 4 = a 5 2
R d = A B . A E . B E 4 d t A B E = a . 5 a 2 4 4. a 2 2 = a 5 8
vậy R = 25 a 64 2 + a 2 4 = a 41 8 .

Đáp án A
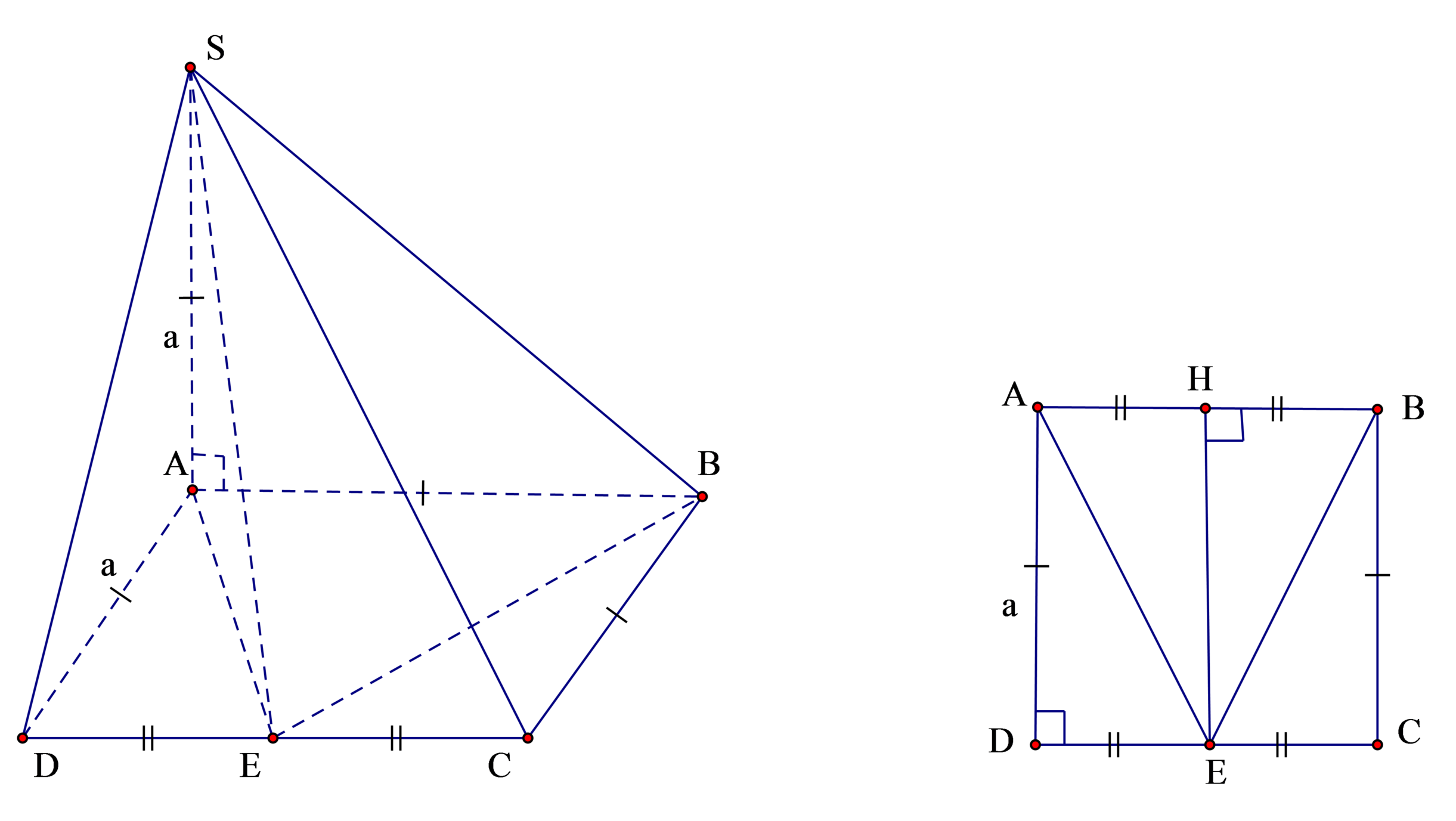
Tam giác ABE cân có A E = B E = a 5 2
và AB = a
⇒ S Δ A B E = a 2 2 = A E . B E . A B 4. R Δ A B E ⇒ R Δ A B E = 2 a . a 5 2 2 : 4 a 2 = 5 a 8
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABE là
R = R Δ A B E 2 + S A 2 4 = 5 a 8 2 + a 2 4 = a 41 8