Cho tứ diện ABCD có AB=AC=AD và góc BAC = góc BAD =\(60^0\)
CMR:a)\(AB\perp CD\)
b)M,N là trung điểm của AB,CD. C/M: \(MN\perp AB,MN\perp CD\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 5 2017
Ta có: A B → . C D → = A B → A D → − A C → = A B → . A D → − A B → . A C →
= A B → . A D → . cos B A D − A B → . A C → cos B A C
= A B 2 . cos 60 ° − A B 2 cos 60 ° (do AB = AC = AD và B A C ^ = B A D ^ = 60 ° )
= 0
Suy ra A B ⊥ C D hay góc giữa hai vecto A B → và C D → là 90 ° .
ĐÁP ÁN C
CM
17 tháng 12 2017
Phương án A sai vì nếu CD ⊥ (ABD) thì CD ⊥ AD. Nhưng tam giác ACD cân tại A nên CD không thể vuông góc với AD
Phương án B sai vì tương tự như trên thì CD không thể vuông góc với AC
Phương án C đúng vì CD ⊥ AN (AN là đường trung tuyến của tam giác cân CAD tại A) và CD ⊥ MN ⇒ CD ⊥ (ABN)
Phương án D sai vì CD không vuông góc với MD do chứng minh trên.
Đáp án C
KH
23 tháng 1 2021
Hình ảnh minh họa , tại e k biết vẽ nhưng A và D = 90 độ và MC=CD , MB=AB . Hình dạng đúng rồi nhưng số đo góc và cạnh k đúng
HP
23 tháng 1 2021
Hình vẽ:
Từ giả thiết ta có \(\dfrac{MC}{MB}=\dfrac{CD}{AB}\left(1\right)\)
Mặt khác \(\left\{{}\begin{matrix}BA\perp AD\\CD\perp AD\end{matrix}\right.\Rightarrow BA//CD\)
\(\Rightarrow\dfrac{CD}{AB}=\dfrac{NC}{NA}\left(2\right)\) (Định lí Talet)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{MC}{MB}=\dfrac{NC}{NA}\)
\(\Rightarrow MN//AB\)
Mà \(AB\perp AD\Rightarrow MN\perp AD\)
CM
12 tháng 4 2018
Tam giác ABD có AB = AD và B A D ^ = 60 °
Nên tam giác ABD đều ⇒ D M = A B 3 2 (DM là trung tuyến)
Tam giác ABC có AB = AC và B A C ^ = 60 °
Nên tam giác ABC đều ⇒ C M = A B 3 2 (CM là trung tuyến)
Do đó: DM = CM nên tam giác MCD cân tại M có MN là trung tuyến (do N là trung điểm của CD)
Suy ra MN là đường cao của tam giác MCD
⇒ M N ⊥ C D
Chứng minh tương tự: ⇒ M N ⊥ C D
Vậy kết luận D là kết luận sai
Đáp án D
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 1 2021
Ta có
\(MN\perp BC;AB\perp BC\) => MN//AB \(\Rightarrow\frac{MN}{AB}=\frac{CM}{CA}\) (Talet trong tam giác)
\(MP\perp AD;CD\perp AD\) => MP//CD \(\Rightarrow\frac{MP}{CD}=\frac{AM}{CA}\) (Talet trong tam giác)
\(\Rightarrow\frac{MN}{AB}+\frac{MP}{CD}=\frac{CM}{CA}+\frac{AM}{CA}=\frac{CA}{CA}=1\left(dpcm\right)\)
26 tháng 10 2018
Xét Tam giác ABC có: N là trung điểm AC, P là trung điểm của AB
=> PM là đường trung bình của tam giác ABC=> PM//=1/2BC
Tương tự: NQ//=1/2 BC
PN//=1/2 AD
MQ//=1/2AD
Mà BC=AD => PM=NQ=PN=MQ=> Tứ giác MPNQ là hình thoi=> MN vuông góc PQ
CM
8 tháng 4 2019
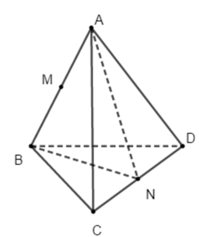
Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)
Đáp án B
Đặt \(AB=AC=AD=x\)
Do \(\widehat{BAC}=60^0\Rightarrow\Delta ABC\) đều \(\Rightarrow BC=x\)
Tương tự tam giác ABD đều \(\Rightarrow BD=x\)
\(\Rightarrow\Delta BCD\) cân tại B
Gọi H là hình chiếu vuông góc của A lên (BCD)
Do \(AB=AC=AD\Rightarrow HA=HB=HC\)
\(\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác
Mà BCD cân tại B \(\Rightarrow BH\perp CD\Rightarrow CD\perp\left(AHB\right)\Rightarrow CD\perp AB\)
b/Từ câu a, do N là trung điểm CD nên N là giao điểm của BH và CD
\(\Rightarrow MN\in\left(ABH\right)\Rightarrow CD\perp MN\)
Lại có: \(\Delta DBC=\Delta DAC\) (c.c.c)
\(\Rightarrow BN=AN\)
\(\Rightarrow\Delta ABN\) cân tại N \(\Rightarrow MN\perp AB\) (trong tam giác cân trung tuyến là đường cao)