cho tam giác abc cân tại a trên nửa mp bờ bc ko chứa a lần lượt vẽ các tia bx, cy sao cho bx ba,cy c. gọi d là giao điểm của các tia bc và cy chứng minh tam giác abd=tam giác acd
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2019
Do tam giác ABC cân tại A nên AB = AC, từ đó tam giác ABD = tam giác ACD (cạnh huyền - cạnh góc vuông).
10 tháng 9 2020
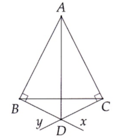
Xét 2 tam giác ABD vuông tại B và tam giác ACD vuông tại C có:
+ Chung cạnh huyền AD
+ AB=AC vì tam giác ABC cân tại A
Vậy 2 tam giác ABD bằng tam giác ACD theo trường hợp (cạnh huyền - cạnh góc vuông)
21 tháng 1 2022
a) Xét Δ ABD vuông tại B và Δ ACD vuông tại C có:
+ AD chung.
+ AB = AC (Tam giác ABC cân tại A).
\(\Rightarrow\Delta ABD=\Delta ACD\) (cạnh huyền - cạnh góc vuông).
b) \(\Delta ABD=\Delta ACD\left(cmt\right).\Rightarrow\) \(\widehat{BDA}=\widehat{CDA}\) (2 góc tương ưng).
\(\Rightarrow\) DA là tia phân giác của \(\widehat{BDC}.\)
22 tháng 11 2023
Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
Mục tiêu -500 sp mong giúp đỡ