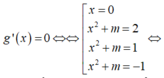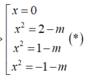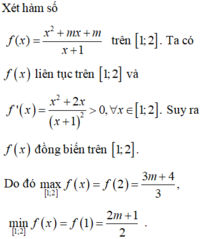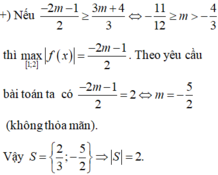Cho y=f(x)=|x2-5x+4|+mx. Gọi S là tập hợp các giá trị nguyên của m sao cho GTNN của f(x) lớn hơn 1. Tính số các phần tử của S.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D.
Xét hàm số f x = x 2 + m x + m x + 1 trên 1 ; 2 , có y ' = x 2 + 2 x x + 1 2 > 0 , ∀ x ∈ 1 ; 2
Suy ra
max 1 ; 2 f x = f 1 ; f 2 = 2 m + 1 2 ; 3 m + 4 3 = 2 m + 1 2 ; 3 m + 4 3
TH1. Với
max 1 ; 2 f x = 2 m + 1 2 = 2 m + 1 = 4 2 m + 1 2 ≥ 3 m + 4 3 ⇔ m = − 5 2 .
TH2:
Với max 1 ; 2 f x = 3 m + 4 3 = 3 m + 4 = 6 2 m + 1 2 ≤ 3 m + 4 3 ⇔ m = 2 3 .

- Xét phương trình hoành độ giao điểm : \(mx-4=-mx-4\)
\(\Leftrightarrow2mx=0\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y=-4\)
=> Tọa độ điểm ( 0; - 4 )
- d1 cắt trục hoành tại điểm : \(\left(\dfrac{4}{m};0\right)\)
- d2 cắt trục hoành tại điểm : \(\left(-\dfrac{4}{m};0\right)\)
=> Tam giác đó là tam giác cân .
\(\Rightarrow S=\dfrac{1}{2}.\left|-4\right|.\left|\dfrac{8}{m}\right|=\left|\dfrac{16}{m}\right|>8\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{16}{m}< -8\\\dfrac{16}{m}>8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\in\left(-2;0\right)\\m\in\left(0;2\right)\end{matrix}\right.\)
Vậy \(S=\left\{1\right\}\)

\(\Leftrightarrow\left(x-y+m\right)^2+y^2+2\left(m+1\right)y-m^2+25\ge0\); \(\forall x;y\)
\(\Leftrightarrow y^2+2\left(m+1\right)y-m^2+25\ge0\) ;\(\forall y\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(-m^2+25\right)\le0\)
\(\Leftrightarrow m^2+m-12\le0\Rightarrow-4\le m\le3\)