Cho ABC, các đường cao BD và CE cắt nhau tại H .Đường vuông góc với AB tại B và đừơng vuông góc với AC tại C cắt nhau tại K.Gọi M là trung điểm của BC.CMR: a) ADB ~ AEC; AED ~ ACB. b) HE.HC = HD. HB c) H,M,K thẳng hàng d) Tam giác ABC phải có điều kiện gì thì tứ giác BACK sẽ là hình thoi? Hình chữ nhật?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC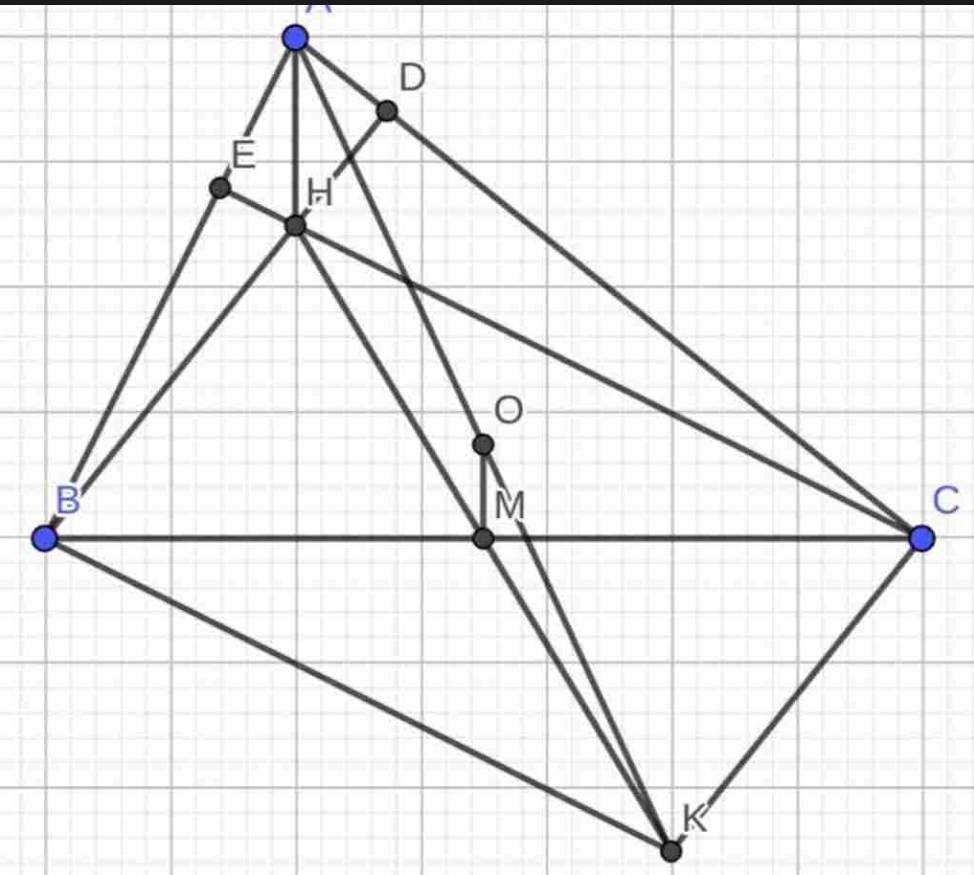

a) xét tam giác ADB và AEC có:
góc A chung
góc ADB= góc AEC (=90 độ)
=> ADB đồng dạng vs AEC (g.g)
b) xét tam giác EHB và tam giác DHC có:
EHB= DHC (2 góc đối đỉnh)
HEB- HDC (=90độ)
=> EHB =DHC (g.g)
=> HE/HB = HD/HC
=> HE.HC=HD.HB

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
b: Xét ΔEHB vuông tại E và ΔDHC vuông tại H có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔEHB\(\sim\)ΔDHC
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)
hay \(HE\cdot HC=HB\cdot HD\)
c: Xét tứ giác HBKC có
HB//KC
HC//BK
Do đó: HBKC là hình bình hành
Suy ra: Hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
hay H,M,K thẳng hàng
a) Xét \(\Delta ADB\)và \(\Delta AEC\)có góc A chung
\(\widehat{ADB}=\widehat{AEC}=90^O\)
\(\Rightarrow\Delta ADB\infty\)( Phần còn lại tương tự nha cậu ^.^ ) \(\Delta AEC\left(g-g\right)\)
b) Xét \(\Delta HEB\)và \(\Delta HDC\)có:
\(\hept{\begin{cases}\widehat{HEB}=\widehat{HDC}=90^O\\\widehat{EHB}=\widehat{DHC\left(đđ\right)}\end{cases}}\)
\(\Rightarrow\Delta HEB\infty\Delta HDC\left(g.g\right)\Rightarrow\frac{HE}{HD}=\frac{4B}{HC}\)
=> HE . HC = HD . HB ( đpcm )
c) Có : \(\hept{\begin{cases}CH\perp AB\\KB\perp AB\end{cases}\Rightarrow KB}//CH\)
TT : HB // CK
=> Tứ giác BHCK là hình bình hành có M là trung điểm BC là 1 đường chéo
=> HK là 1 đường chéo đi qua M
=> H,K,M thẳng hàng
d) BHCK là hình thoi <=> CH = HB <=> \(\Delta EHB=\Delta DHK\)
=> EB = DC => \(\Delta EBC=\Delta DCB\Rightarrow\widehat{EBC}=\widehat{DCB}\)
=> \(\Delta ABC\)cân tại A
BHCK là hình chữ nhật thì \(\widehat{HCK}=90^O\)
<=> HC \(\perp\)KC <=> H \(\in\)AC ( theo gt )
=> \(\Delta ABC\)đều (đpcm )
a) ADB và AEC có: ^A chung
^ADB = ^AEC (=90o)
=> ADB~AEC
=> góc ABD=gócACE
EDCD nội tiếp đường tròn => gócDEC=gócDBC
mà góc ADE = ^DEC + ^ACE (góc ngoài tg)
và góc ABC = ^DBC + ^ABD
Do đó: ^ADE = ^ABC
AED và ACB có: ^A chung ; ^ADE = ^ABC => đồng dạng (gg)
b,
Xét tam giác HEB và tam giác HDC có
góc HEB= góc HDC (=90 độ)
góc EHB= góc DHC ( đối đỉnh)
=>tam giácHEB đồng dạng tam giác HDC(g.g)
=>HE/HD=HB/HC
<=> HE.HC= HD.HB
c)
Có BD vuông góc AC
CK vuông góc AC
=> BD song song CK hay BH song song CK
Có CE vuông góc AB
BK vuông góc AB
=> CE song song BK hay CH song song BK
Tứ giác BHCK có BH song song CK
CH song song BK
=> BHCK là hbh ( dhnb)
Mà M là trung điểm của đg chéo BC
=> M cũng là trung điểm của đg chéo HK
=> H,M,K thẳng hàng
d) BK ⊥ AB và CH ⊥ AB
=> BK // CH
+ Tương tự : CK // BH
=> Tứ giác BHCK là hình bình hành
Do đó tứ giác BHCK là hình thoi
<=> BC ⊥ HK
<=> HM ⊥ BC ( do H,M,K thẳng hàng )
<=> AM là đường trung tuyến đồng thời là đường cao của tam giác ABC
<=> Tam giác ABC cân tại A
+ Tứ giác BHCK là hình chữ nhật
<=> CH ⊥ CK ( hình bình hành có 1 góc vuông là hình chữ nhật )
<=> CH trùng với CA
<=> CA ⊥ AB ( do CH ⊥ AB )
<=> tam giác ABC vuông tại A