Cho tam giác ABC có góc A bằng 68°.Hai đường phân giác BE và CF cắt nhau tại G.Tính góc BGF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bn vào link này ạ:
Https://olm.vn/hoi-dap/detail/250396270588.html
Hok tốt
ta có: A+ABC+BCA=180(Định lí tổng 3 góc của 1 tam giác)
ABC+BCA=180-A
ABC+BCA=112
ta có:GBC=1/2ABC
GCB=1/2BCA
GCB+BCA=1/2ABC+1/2BCA=1/2(ABC+BCA)=1/2*112=56
Ta lại có: BGF=GCB+BCA(ĐL góc ngoài của tam giác)
-->BGF=56
mk thiếu kí hiệu góc và độ nha bạn

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
BE=CF
\(\widehat{ABE}=\widehat{ACF}\)
Do đó: ΔABE=ΔACF
SUy ra: AB=AC
hay ΔABC cân tại A
b: Xét ΔAFH vuông tại F và ΔAEH vuông tại E có
AH chung
AE=AF
Do đó: ΔAFH=ΔAEH
Suy ra: \(\widehat{FAH}=\widehat{EAH}\)
hay AH là tia phân giác của góc BAC

góc ABC+góc ACB=180-60=120 độ
=>góc IBC+góc ICB=60 độ
=>góc EIC=60 độ

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
b) Ta có: ΔAEB\(\sim\)ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)

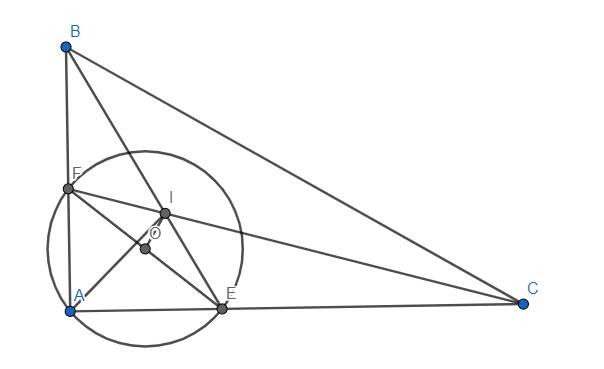
Theo tính chất quen thuộc, O là tâm của (AEF).
Mặt khác, ta lại có \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=135^o\) nên \(\widehat{BIF}=45^o\). Lại có \(\widehat{BAI}=45^o\) nên \(\Delta BIF~\Delta BAI\left(g.g\right)\) \(\Rightarrow\dfrac{BI}{BA}=\dfrac{BF}{BI}\Rightarrow BI^2=BA.BF\) \(\Rightarrow P_{B/\left(O\right)}=P_{B/\left(I;0\right)}\)
\(\Rightarrow\) B nằm trên trục đẳng phương của (O) và (I;0).
Hoàn toàn tương tự, ta chứng minh được C nằm trên trục đẳng phương của (O) và (I;0). Từ đó suy ra BC là trục đẳng phương của (O) và (I;0) \(\Rightarrow BC\perp OI\) (đpcm)
180-68=112
112/2=56
vậy BGF=56 độ
Cho tam giác ABC có góc A bằng 68.Hai đường phân giác BE và CF cắt nhau tại G. tính góc BGF