cho xôy =120, điểm A thuộc tia phân giác của góc đó, kẻ AB vuông góc 0x (B thuộc 0x), kẻ AC vuông góc 0y (C thuộc 0y) chứng minh tam giác ABC là tam giác đều?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 2 2022
Xét ΔABO vuông tại B và ΔACO vuông tại C có
OA chung
\(\widehat{BOA}=\widehat{COA}\)
Do đó: ΔABO=ΔACO
Suy ra: AB=AC
hay ΔABC cân tại A
mà \(\widehat{CAB}=180^0-120^0=60^0\)
nên ΔABC đều
15 tháng 1 2016
Bài này mình biết làm nhưng không biết vẽ hình trên máy tính
17 tháng 11 2016
Ta có hình vẽ:
Δ OBA vuông tại B có: A1 + O1 = 90o (1)
Δ OCA vuông tại C có: A2 + O2 = 90o (2)
Từ (1) và (2) lại có: O1 = O2 vì OA là phân giác của BOC
=> A1 = A2
Xét Δ OBA và Δ OCA có:
A1 = A2 (cmt)
OA là cạnh chung
O1 = O2 (cmt)
Do đó, Δ OBA = Δ OCA (c.g.c)
=> AB = AC (2 cạnh tương ứng)
=> Δ ABC là tam giác cân tại A
12 tháng 5 2019
C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
12 tháng 5 2019
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm
20 tháng 4 2017
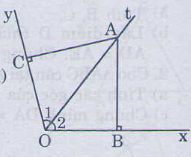
Hai tam giác vuông ACO và ABO có:
ˆO1O1^=ˆO2O2^(gt)
AO chung
Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)
Suy ra AC=AB.
Vây ∆ABC là tam giác cân(AB=AC).
8 tháng 12 2016
Hình thím tự vẽ:
(tại cái bài lúc nãy đang làm gần xong cái tự nhiên "Ôi hỏng!!")
Gọi M là giao điểm của OA và BC
-Xét tam giác OAB và tam giác OAC có:
\(\widehat{AOB}\)=\(\widehat{AOC}\) (GT)
OA: cạnh chung
\(\widehat{B}\)=\(\widehat{C}\)=900 (GT)
=> tam giác OAB = tam giác OAC
(theo trường hợp cạnh huyền góc nhọn)
Ta có: OA là phân giác góc O
\(\widehat{AOB}\)=\(\widehat{AOC}\) = \(\frac{1}{2}\)\(\widehat{O}\) = \(\frac{1}{2}\)1200 = 600
Trong tam giác OAB có:
\(\widehat{O}\)+\(\widehat{A}\)+\(\widehat{B}\)=1800 (tổng 3 góc trong tam giác)
hay 600 + góc A + 900 = 1800
=> \(\widehat{A}\) = 300
Vì tam giác OAB = tam giác OAC
nên \(\widehat{OAB}\)=\(\widehat{OAC}\)=300
-Xét tam giác ABM và tam giác ACM có:
AM: cạnh chung
\(\widehat{BAM}\)=\(\widehat{CAM}\) (tam giác OAB = tam giác OAC)
AB = AC (tam giác OAB = tam giác OAC)
=> tam giác ABM = tam giác ACM (c.g.c)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)
Mà \(\widehat{AMB}\)+\(\widehat{AMC}\) = 1800 (kề bù)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\)=900
Trong tam giác ABM có:
\(\widehat{BAM}\)+\(\widehat{ABM}\)+\(\widehat{AMB}\)=1800 (tổng 3 góc của tam giác)
hay 300 + góc ABM + 900 = 1800
=> \(\widehat{ABM}\)=600
Vì tam giác ABM = tam giác ACM
nên \(\widehat{ABM}\)=\(\widehat{ACM}\)=600 (2 góc tương ứng)
Ta có: \(\widehat{BAM}\)+\(\widehat{CAM}\)=300+300=600
Trong tam giác ABC có:
\(\widehat{BAC}\)=\(\widehat{ABC}\)=\(\widehat{ACB}\)=600
=> tam giác ABC là tam giác đều
Vậy tam giác ABC là tam giác đều
"Sorry, hôm nay tớ bực bội wa"
8 tháng 12 2016
\(\Delta BOA\)vuông tại B có: BOA + OAB = 90o
\(\Delta COA\)vuông tại C có: COA + OAC = 90o
Mà BOA = COA vì OA là tia phân giác của BOC
=> OAB = OAC
Xét \(\Delta BOA\) và \(\Delta COA\) có:
BOA = COA (cmt)
OA là cạnh chung
BAO = CAO (cmt)
Do đó, \(\Delta BOA=\Delta COA\left(c.g.c\right)\)
=> AB = AC (2 cạnh tương ứng)
Như vậy tam giac ABC cân tại A