giải phương trình sau
(x-1)(x2+2x-6)=x3-1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(6+2x\ge3-x\)
\(\Leftrightarrow3x\ge-3\)
\(\Leftrightarrow x\ge-1\)
2.
\(2x+7>16-x\)
\(\Leftrightarrow3x>23\)
\(\Leftrightarrow x>\dfrac{23}{3}\)
3.
\(x-5< 3x+1\)
\(\Leftrightarrow2x>-6\)
\(\Leftrightarrow x>-3\)
Mik chưa học đến lớp 8 nên ko bt biểu diễn trên trục số nên chỉ tìm dc x thôi nha:
1. 6 + 2x \(\ge\) 3 - x
<=> 6 - 3 \(\ge\) -x - 2x
<=> 3 \(\ge\) -3x
<=> 3 : (-3) \(\ge\) -3x : (-3)
<=> -1 \(\le\) x
<=> x \(\ge\) -1
2. 2x + 7 > 16 - x
<=> 2x + x > 16 - 7
<=> 3x > 9
<=> 3x : 3 > 9 : 3
<=> x > 3
3. x - 5 < 3x + 1
<=> -5 - 1 < 3x - x
<=> -6 < 2x
<=> -6 : 2 < 2x : 2
<=> -3 < x
<=> x > (-3)

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
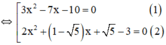
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
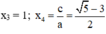
Vậy phương trình có tập nghiệm 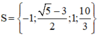
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
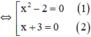
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
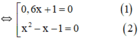
+ Giải (1): 0,6x + 1 = 0 ⇔ 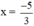
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 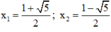
Vậy phương trình có tập nghiệm 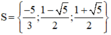
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔...

a:
Sửa đề: \(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\)
=>x^2+x+1-3x^2=2x(x-1)
=>-2x^2+x+1-2x^2+2x=0
=>-4x^2+3x+1=0
=>4x^2-3x-1=0
=>4x^2-4x+x-1=0
=>(x-1)(4x+1)=0
=>x=1(loại) hoặc x=-1/4(nhận)
b: =>2x+6x=x+3(2x+1)
=>x+6x+3=8x
=>7x+3=8x
=>-x=-3
=>x=3(nhận)

Không dich được đề bài, đề là:
\(\dfrac{2x^2-1}{x^3+1}+\dfrac{1}{x+1}=2x\left(\dfrac{1-x^2-x}{x^2-x+1}\right)\)
Hay: \(...=2\left(1-x^2-\dfrac{x}{x^2-x+1}\right)\)

i,<=>(2x - 1)(2x - 1 + 2 - x) = 0 <=> (2x - 1)(x + 1) = 0
<=> x = 1/2 hoặc x = -1
j,<=>(x - 1)(5x + 3) - (3x - 5)(x - 1) = 0
<=>(x - 1)(2x + 8) = 0 <=> x = 1 hoặc x = -4
k,<=>4(x + 5)(x - 6) = 0 <=> (x + 5)(x - 6) = 0
<=> x = -5 hoặc x = 6
m,<=>x^2(x + 1) + x + 1 = 0
<=>(x^2 + 1)(x + 1) = 0 (1)
Mà x^2 + 1 > 0 với mọi x nên (1) xảy ra <=> x + 1 = 0
<=> x = -1

Ta có: x - 1 3 + 2x = x 3 – x 2 – 2x +1
⇔ x 3 – 3 x 2 + 3x - 1 + 2x = x 3 – x 2 - 2x + 1
⇔ 2 x 2 – 7x +2 =0
∆ = - 7 2 -4.2.2 = 49 - 16 = 33 > 0
∆ = 33
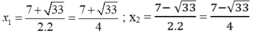

Bài 6:
1) Ta có: \(2x\left(x-5\right)-\left(x+3\right)^2=3x-x\left(5-x\right)\)
\(\Leftrightarrow2x^2-10x-\left(x^2+6x+9\right)=3x-5x+x^2\)
\(\Leftrightarrow2x^2-10x-x^2-6x-9-3x+5x-x^2=0\)
\(\Leftrightarrow-14x-9=0\)
\(\Leftrightarrow-14x=9\)
\(\Leftrightarrow x=-\dfrac{9}{14}\)
Vậy: \(S=\left\{-\dfrac{9}{14}\right\}\)
`1)2x(x-5)-(x+3)^2=3x-x(5-x)`
`<=>2x^2-10x-x^2-6x-9=3x-5x+x^2`
`<=>x^2-16x-9=x^2-2x`
`<=>14x=-9`
`<=>x=-9/14`

4) Ta có: \(\dfrac{2x-5}{5}-\dfrac{x+3}{3}=\dfrac{2-3x}{2}-x-2\)
\(\Leftrightarrow\dfrac{6\left(2x-5\right)}{30}-\dfrac{10\left(x+3\right)}{30}=\dfrac{15\left(2-3x\right)}{30}-\dfrac{30\left(x+2\right)}{30}\)
\(\Leftrightarrow12x-30-10x-30=30-45x-30x-60\)
\(\Leftrightarrow-22x-60=-75x-30\)
\(\Leftrightarrow-22x+75x=-30+60\)
\(\Leftrightarrow53x=30\)
\(\Leftrightarrow x=\dfrac{30}{53}\)
Vậy: \(S=\left\{\dfrac{30}{53}\right\}\)
5) Ta có: \(\dfrac{5x-3}{6}-\dfrac{7x-1}{4}=5\)
\(\Leftrightarrow\dfrac{2\left(5x-3\right)}{12}-\dfrac{3\left(7x-1\right)}{12}=\dfrac{60}{12}\)
\(\Leftrightarrow10x-6-21x+3=60\)
\(\Leftrightarrow-11x-3=60\)
\(\Leftrightarrow-11x=63\)
\(\Leftrightarrow x=-\dfrac{63}{11}\)
Vậy: \(S=\left\{-\dfrac{63}{11}\right\}\)
`9,x^3+x^2-2=0`
`x^3-x^2+2x^2-2=0`
`<=>x^2(x-1)+2(x-1)(x+1)=0`
`<=>(x-1)(x^2+2x+2)=0`
`<=>x=1`
`14,x^2-2x+1=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
`15,x^3+3x^2+3x+1=0`
`<=>(x+1)^3=0`
`<=>x+1=0`
`<=>x=-1`

1: \(\Leftrightarrow\left(x-3\right)\left(x+3\right)-\left(x-3\right)\left(5x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(-4x+1\right)=0\)
hay \(x\in\left\{3;\dfrac{1}{4}\right\}\)
2: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2x+16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1-x^2+2x-16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-15\right)=0\)
hay \(x\in\left\{1;5\right\}\)
3: \(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-1\right)\left(2x+1\right)=0\)
hay \(x\in\left\{1;\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
4: \(\Leftrightarrow x^2\left(x+4\right)-9\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{-4;3;-3\right\}\)
5: \(\Leftrightarrow\left[{}\begin{matrix}3x+5=x-1\\3x+5=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-6\\4x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
6: \(\Leftrightarrow\left(6x+3\right)^2-\left(2x-10\right)^2=0\)
\(\Leftrightarrow\left(6x+3-2x+10\right)\left(6x+3+2x-10\right)=0\)
\(\Leftrightarrow\left(4x+13\right)\left(8x-7\right)=0\)
hay \(x\in\left\{-\dfrac{13}{4};\dfrac{7}{8}\right\}\)
1.
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(5x-2\right)\)
\(\Leftrightarrow x+3=5x-2\)
\(\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\)
2.
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=\left(x-1\right)\left(x^2-2x+16\right)\)
\(\Leftrightarrow x^2+x+1=x^2-2x+16\)
\(\Leftrightarrow3x=15\Leftrightarrow x=5\)
3.
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2};x=-\dfrac{1}{2}\end{matrix}\right.\)
(x-1)(x2+2x-6)=x3-1
<=> x3 + 2x2 - 6x - x2 - 2x + 6 = x3 - 1
<=> x3 + 2x2 - 6x - x2 - 2x + 6 - x3 + 1 = 0
<=> x2 - 8x + 7 = 0
<=> x2 - x - 7x + 7 = 0
<=> ( x - 1 )( x - 7 ) = 0
Giải nốt
\(\left(x-1\right)\left(x^2+2x-6\right)=x^3-1\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2x-6\right)-\left(x^3-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2x-6\right)-\left(x-1\right)\left(x^2+x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x^2+2x-6\right)-\left(x^2+x+1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2x-6-x^2-x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-7\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=7\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{1;7\right\}\)